Den grundlegenden Kalkül der Begriffslogik gewinnt man nach einem einfachen Rezept:
Man nehme einen Kalkül, der genau der Struktur ,,Boolescher Verband``
entspricht und ergänze ihn durch verallgemeinerte Operationen ![]() und
und
![]() ,
deren Regeln denjenigen von Infimum und Supremum in Vollständigen
(Booleschen) Verbänden nachgebildet sind; dies ergibt den Kalkül VBV. Sodann
gestatte man, daß die Variablen dieses Kalküls nicht nur für Terme, sondern
auch für beliebige Formeln (siehe Abschnitt 2.1) stehen dürfen;
ergibt BL (=Begriffslogik). Weiter füge man eine sog. Deduktions- und
Abtrennungsregel hinzu; ergibt BL
,
deren Regeln denjenigen von Infimum und Supremum in Vollständigen
(Booleschen) Verbänden nachgebildet sind; dies ergibt den Kalkül VBV. Sodann
gestatte man, daß die Variablen dieses Kalküls nicht nur für Terme, sondern
auch für beliebige Formeln (siehe Abschnitt 2.1) stehen dürfen;
ergibt BL (=Begriffslogik). Weiter füge man eine sog. Deduktions- und
Abtrennungsregel hinzu; ergibt BL![]() .
.
Der Zusatz des sog. Urteilsprinzips liefert die (volle) Urteilslogik: den
Kalkül BL
![]() .
Dieser entspricht der Aussagen- und
Prädikatenlogik (erster Stufe).
.
Dieser entspricht der Aussagen- und
Prädikatenlogik (erster Stufe).
Andere Zusätze liefern natürlich andere ,,Abkömmlinge`` des ,,Stamm-Kalküls``. Entsprechend ergibt sich eine andere Hierachie, wenn man statt von VBV von einem anderen Kalkül ausgeht (siehe Abb. 1, die Übersicht, sowie insbesondere Abschitt 2.10 zum Übergang von VBV nach BL die Definition von Beziehungs- und Verknüpfungszeichen).
Es folgt nun zunächst die Beschreibung der sog. ,,Formalen Sprache`` (des ,,Vokabulars``, des ,,Wortschatzes``) für die Kalküle VBV, BL, etc.:
| Grundzeichen | a b c ... | Variablen | |
| A B C ... | |||
| 0 1 | Konstanten | ||
| Beziehungszeichen | |||
| |
Verknüpfungszeichen |
| Ausdrücke | Terme |
| 1. Zeichen des Alphabetes (Variablen und Konstanten), die
auch (mehrfach) mit Indizes oder Exponenten (aus dem Alphabet) versehen sein
dürfen; (sowie Ausdrücke der Gestalt |
|
| 2. Sind |
| v-Formeln (=verbandstheoretische Formeln) | |
| Sind |
| l-Formeln (=logische Formeln) | |
| 1. wie Terme 1. | |
| 2. Sind |
Die eindeutige Lesbarkeit der Ausdrücke wird nötigenfalls durch Setzen von Klammern gewährleistet.
Zwecks Anwendung der Kalküle darf die Formale Sprache durch geeignete
Zeichen(-Kombinationen) erweitert werden, so daß etwa auch
![]() ,
,
![]() (als Abkürzung für
(als Abkürzung für
![]() )
u.ä. zulässige Ausdrücke wären (cf. Computersprache
PROLOG). Wir denken uns in einem solchen Falle die Ausdrucks-Definition
entsprechend angepaßt.
)
u.ä. zulässige Ausdrücke wären (cf. Computersprache
PROLOG). Wir denken uns in einem solchen Falle die Ausdrucks-Definition
entsprechend angepaßt.
Es folgen die Axiome (=Grundformeln und Grundregeln) für die Kalküle VBV und BL:
(Ableitbare / beweisbare Formeln und Regeln nennen wir Theoreme bzw. Sätze.)
| Grundformeln | Grundregeln | VBV, BL |
| 1 | 5 |
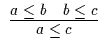 |
||||||
| 2 |
|
6 |
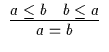 |
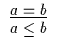 |
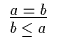 |
|||
|
|
| 3 | 7 |
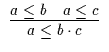 |
|||||
| 4 | 8 |
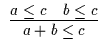 |
||||||
| 9 |
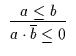 |
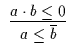 |
||||||
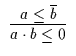 |
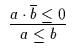 |
|||||||
| 2' |
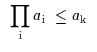 |
7' |
![$\begin{array}{c}\infer[{\rm iNFa}]{a \leq \; \displaystyle{\prod_{\rm {i}}{b_{\rm {i}}}}}{a \leq b_{i}}\end{array}$](img50.gif) |
| 3' |
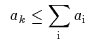 |
8' |
![$\begin{array}{c}\infer[{\rm iNFb}]{\displaystyle{\sum_{\rm {i}}{a_{\rm {i}}}} \leq b}{a_{i} \leq b}\end{array}$](img52.gif) |
| 2'' |
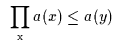 |
7'' |
![$\begin{array}{c}\infer[{\rm xNFa}]{a \leq \displaystyle{\prod_{\rm {x}}{b(x)}}}{a \leq b(x)}\end{array}$](img54.gif) |
| 3'' |
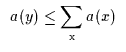 |
8'' |
![$\begin{array}{c}\infer[{\rm xNFb}]{\displaystyle{\sum_{\rm {x}}{a(x)}} \leq b}{a(x) \leq b}\end{array}$](img56.gif) |
Es folgt ein Kalkül, der die Bedeutung von ,,![]() kommt nicht frei in ...
vor`` (
kommt nicht frei in ...
vor`` (![]() NF
NF![]() ) festlegt:
) festlegt:
| NF - Kalkül5 | ||||
Läßt man eine der vier Negationsregeln (9) weg, so ergibt sich eine
schwächere Negation,
![]() ist nicht mehr
beweisbar.
ist nicht mehr
beweisbar.
Auch sind nicht nur Abwandlungen der Negationsregeln von Interesse, sondern auch solche, bei denen etwa die Distributiv-Gesetze nicht mehr gelten (cf. Quanten-Physik) u.ä.
Beim verbandstheoretischen Kalkül VBV (= Vollständiger Boolescher Verband) steht
| jeweils für einen beliebigen Term , | ||
| für einen Term, der (gegebenenfalls) den variablen Index |
||
| für einen Term, der (gegebenenfalls) den konstanten bzw.
variablen Index |
||
| für einen Term, der (gegebenenfalls) die freie Variable |
||
| für einen Term, der (gegebenenfalls) den Term |
(,,gegebenenfalls`` soll jeweils heißen: Index bzw. Variable brauchen in dem
betreffenden Ausdruck überhaupt nicht vorkommen, oder sie kommen nur
nicht-frei vor, so daß etwa
![]() ein Spezialfall
von 2' ist etc.)
ein Spezialfall
von 2' ist etc.)
Für die logischen Kalküle BL (= Begriffslogik), BL![]() etc. gilt
dasselbe, wenn man statt ,,Term`` überall ,,l-Formel`` sagt.
etc. gilt
dasselbe, wenn man statt ,,Term`` überall ,,l-Formel`` sagt.
Zwei Beispiele sollen andeuten, was man unter einem Beweis bzw. einer Ableitung in obigen Kalkülen zu verstehen hat:
|
|
|
|
Dabei ist ,,![]() ,
,
![]() ,
...
,
... ![]()
![]() `` zu lesen als: ,,Aus den
Prämissen/Annahmen
`` zu lesen als: ,,Aus den
Prämissen/Annahmen ![]() ,
, ![]() ,
... ist beweisbar/ableitbar (in dem
betreffenden Kalkül) die Konklusion
,
... ist beweisbar/ableitbar (in dem
betreffenden Kalkül) die Konklusion ![]() ``, und zwar unter Verwendung von
Grundformeln und -Regeln bzw. bereits bewiesenen Formeln und Regeln dieses
Kalküls.
``, und zwar unter Verwendung von
Grundformeln und -Regeln bzw. bereits bewiesenen Formeln und Regeln dieses
Kalküls.
| steht als Abkürzung für die beiden Beweise | ||
| etwa steht entsprechend für einen
Beweis in beiden Richtungen. |
Wichtige Sätze der Kalküle VBV und BL, auf deren Beweis wir hier verzichten:
Die Definitionen der verschiedenen Arten von Kalkül-Ausdrücken lassen sich ihrerseits noch etwas kalkülmäßiger notieren: Man könnte Begriffe wie Var, Konst, Alph, Term etc. einführen und die entsprechenden Definitionen regelartig schreiben, z.B.:
| Term( |
Term( |
|
| Var( |
Ein Kalkül K bestünde dann u.a. aus drei Teilen:
Auf den Wortkalkül stützt sich die (Meta-)Beweismethode der Induktion nach der Länge/Komplexität der Ausdrücke, während sich die Methode der Induktion nach der Länge/Komplexität von Beweisen auf den Beweiskalkül bezieht.
Die Prüfung etwa, ob ein bestimmter Ausdruck ein Term ist, wenn gewisse andere Ausdrücke Terme sind o.ä., verliefe dann ähnlich wie z.B. der Nachweis im Schlußkalkül, daß eine bestimmte Formel aus gewissen Annahmen beweisbar ist etc.
Übrigens könnte man die Ausdrucksdefinitionen, die Axiome und den NF-Kalkül klammerreicher formulieren, etwa so:
Sind ![]() und
und ![]() Terme, so auch
Terme, so auch
![]() ,
,
![]() ,
,
![]() etc.
etc.
Sind ![]() und
und ![]() l-Formeln, so auch
l-Formeln, so auch ![]() etc.
etc.
![]() ;
;
![]() ,
,
![]()
![]()
![]() etc.
etc.
![]() NF
NF![]() ,
,
![]() NF
NF![]()
![]()
![]() NF
NF
![]() ,
...
,
... ![]() NF
NF![]() etc.
etc.
Für den Alltagsgebrauch wird dann festgelegt, in welcher Reihenfolge bestimmte Zeichen ,,binden`` bzw. ,,trennen`` und welche Klammern demnach wegfallen können.
Es heißt gelegentlich, die Ausdrücke eines Kalküls (,,Syntax``) seien bedeutungslos, es müßte ihnen eine Bedeutung erst mit Hilfe einer ,,Semantik`` oder ,,Modelltheorie`` zugeordnet werden. In einem einfachen Falle ist die Lage etwa folgende:
Man arbeitet mit drei Systemen S![]() ,
S
,
S![]() und S
und S![]() .
S
.
S![]() ist voll oder weitgehend formalisiert: der bedeutungslose,
syntaktische Kalkül (K
ist voll oder weitgehend formalisiert: der bedeutungslose,
syntaktische Kalkül (K![]() ). S
). S![]() ist weniger, S
ist weniger, S![]() ,
der Meta-Kalkül, der als Grundlage zum Vergleich von S
,
der Meta-Kalkül, der als Grundlage zum Vergleich von S![]() und
S
und
S![]() dient, meist am wenigsten formalisiert.
dient, meist am wenigsten formalisiert.
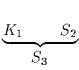
Den als bedeutungslos angenommenen Ausdrücken von K![]() wird nun
vermöge einer homomorphen (d.h. in einem bestimmten Sinne
Struktur-erhaltenden) Abbildung (,,Interpretation``) je eine Bedeutung aus
dem System S
wird nun
vermöge einer homomorphen (d.h. in einem bestimmten Sinne
Struktur-erhaltenden) Abbildung (,,Interpretation``) je eine Bedeutung aus
dem System S![]() zugeordnet, etwa durch eine Formel der Gestalt
h(A) = B o.ä.
zugeordnet, etwa durch eine Formel der Gestalt
h(A) = B o.ä.
Was aber ist mit den Ausdrücken der Systeme S![]() und S
und S![]() ?
?
Besitzen sie - weil gar nicht bzw. weniger formal - ,,von Natur aus`` gewisse Bedeutung(en) und bedürfen also keiner besonderen Bedeutungszuordnung?
Man könnte nun versuchen, S![]() und S
und S![]() ihrerseits
(weitgehend) zu formalisieren. Gesetzt, das sei gelungen, so ergibt sich
genau genommen:
ihrerseits
(weitgehend) zu formalisieren. Gesetzt, das sei gelungen, so ergibt sich
genau genommen:
Es werden zwei Kalküle K![]() und K
und K![]() auf dem Hintergrund
eines Meta-Kalküls K
auf dem Hintergrund
eines Meta-Kalküls K![]() miteinander verglichen.
miteinander verglichen.
Letzterer ist meist ziemlich stark, umfaßt Aussagen- und Prädikatenlogik nahezu beliebiger Stufe, Vollständige Induktion, Mengenlehre u.ä.
Ein Beispiel mag dieses illustrieren:
K![]() sei ein (syntaktischer) aussagenlogischer Formalismus;
S
sei ein (syntaktischer) aussagenlogischer Formalismus;
S![]() ,
die zugehörige Semantik, sei gegeben durch den Apparat der
,,Wahrheitstafeln`` oder die zweielementige Boolesche Algebra über
,
die zugehörige Semantik, sei gegeben durch den Apparat der
,,Wahrheitstafeln`` oder die zweielementige Boolesche Algebra über ![]() .
.
Wir denken uns nun S![]() hinreichend kalkülisiert durch K
hinreichend kalkülisiert durch K![]() (etwa einen Gleichungskalkül) und ebenso S
(etwa einen Gleichungskalkül) und ebenso S![]() durch K
durch K![]() .
.
Die bekannten Sätze über die semantische Widerspruchsfreiheit und Vollständigkeit der Aussagenlogik scheinen nun folgende Beweise zu erfordern:
| Widerspruchsfreiheit: |
|
| Vollständigkeit: |
|
Genaugenommen wurden hier lediglich die Kalküle K![]() und K
und K![]() miteinander verglichen und als in einem bestimmten Sinne äquivalent (siehe
Abschnitt 4) erwiesen. (Es kann im allgemeinen Fall übrigens
auch vorkommen, daß der ,,Urbild-Kalkül`` schwächer ist als der
,,Bild-Kalkül``; man spricht dann von Unvollständigkeit.)
miteinander verglichen und als in einem bestimmten Sinne äquivalent (siehe
Abschnitt 4) erwiesen. (Es kann im allgemeinen Fall übrigens
auch vorkommen, daß der ,,Urbild-Kalkül`` schwächer ist als der
,,Bild-Kalkül``; man spricht dann von Unvollständigkeit.)
Es scheint also nicht zu gelingen, die Zeichenebene, die ,,Welt der Kalküle``
zu verlassen, um die ,,Bedeutungen selbst`` zu erreichen. In diesem
Zusammenhang könnte man noch fragen, ob der Kalkül K![]() ein reiner
Gleichungskalkül sein kann oder ob man nicht Teile der Aussagenlogik, also
des Kalküls K
ein reiner
Gleichungskalkül sein kann oder ob man nicht Teile der Aussagenlogik, also
des Kalküls K![]() ,
wie etwa die Negation u.a. zu seinem
Funktionieren benötigt.
,
wie etwa die Negation u.a. zu seinem
Funktionieren benötigt.
Auch wird auf dem Hintergrund der soeben skizzierten Ansicht der gelegentlich behauptete Vorrang der semantischen vor der syntaktischen Darstellung (der Aussagenlogik) zweifelhaft.
Weiterhin ließe sich im Sinne obiger Sichtweise nach der syntaktischen
Widerspruchsfreiheit von K![]() und K
und K![]() fragen (also nach der
Unmöglichkeit von
fragen (also nach der
Unmöglichkeit von ![]()
![]() ,
, ![]()
![]() ).
).
Gesetzt, sie sei bewiesen, dann fragt sich weiter, mit welchen Beweis-Mitteln?
Nach Voraussetzung mit den Mitteln von K![]() .
.
K![]() jedoch ist beträchtlich stärker als etwa K
jedoch ist beträchtlich stärker als etwa K![]() ,
und so
hätte man die Widerspruchsfreiheit des schwächeren, also weniger der
Widersprüchlichkeit verdächtigen Kalküls mit den Mitteln des stärkeren,
also eher verdächtigen bewiesen (cf. auch Gödels Zweiten Satz).
,
und so
hätte man die Widerspruchsfreiheit des schwächeren, also weniger der
Widersprüchlichkeit verdächtigen Kalküls mit den Mitteln des stärkeren,
also eher verdächtigen bewiesen (cf. auch Gödels Zweiten Satz).
Wie aber beweist man die Widerspruchsfreiheit von K![]() etc. ?
etc. ?
Und was bedeuten all solche Beweise, was zeigen sie ,,eigentlich``?
In den üblichen Darstellungen sind semantisches (S![]() )
und
Meta-System (S
)
und
Meta-System (S![]() )
i.a. - soweit ich sehe - halbformal und werden
anscheinend als ,,unbedenklich`` betrachtet.
)
i.a. - soweit ich sehe - halbformal und werden
anscheinend als ,,unbedenklich`` betrachtet.
Vor dem weiteren Ausbau der Kalküle VBV und BL wollen wir noch der Frage nachgehen, ob man ohne Rückgriff auf irgendeine Deutung rein Kalkül-intern Beziehungszeichen von Verknüpfungszeichen unterscheiden kann.
Hierbei hilft folgende Beobachtung weiter: In einem (halbformalen)
arithmetischen Beweis wird man nie Ausdrücke der Gestalt ![]() ,
,
![]() o.ä. allein antreffen, wohl aber solche der Form
o.ä. allein antreffen, wohl aber solche der Form ![]() zum
Beispiel. Andererseits kommen etwa Ausdrücke der Gestalt
zum
Beispiel. Andererseits kommen etwa Ausdrücke der Gestalt ![]() überhaupt nicht vor. Dies ,,legt`` folgende Definition ,,nahe``:
überhaupt nicht vor. Dies ,,legt`` folgende Definition ,,nahe``:
Der Leser möge nun folgendes nachprüfen:
Für (noch-)nichtlogische Kalküle scheint eine solche Trennung charakteristisch zu sein (cf. die Unterscheidung von v-Formeln und l-Formeln).
Dies entspricht dem Umstand, daß in der Logik die Beziehung von Grundobjekten wiederum ein Grundobjekt ist, d.h. die Beziehung von Begriffen ist wieder ein Begriff, die Beziehung von Urteilen ist wieder ein Urteil. Dagegen ist z.B. die Beziehung etwa zweier Zahlen keine Zahl.
D.h. obige Definition bietet eine Handhabe zur Unterscheidung von (noch-)nichtlogischen und logischen, sowie von begriffs- und urteilslogischen Kalkülen auf rein syntaktischer Ebene.