Ein weiterer Ausbau der Begriffslogik kann nun auf Zusammenhänge führen, wie sie etwa in der folgenden Übersicht (Abb. 1) dargestellt sind. Die Spitzen der durchgezogenen Pfeile zeigen jeweils auf die durch Hinzufügen von Axiomen entstandenen, stärkeren Kalküle. Unterbrochene Linien deuten auf einen eigens zu beweisenden Zusammenhang.
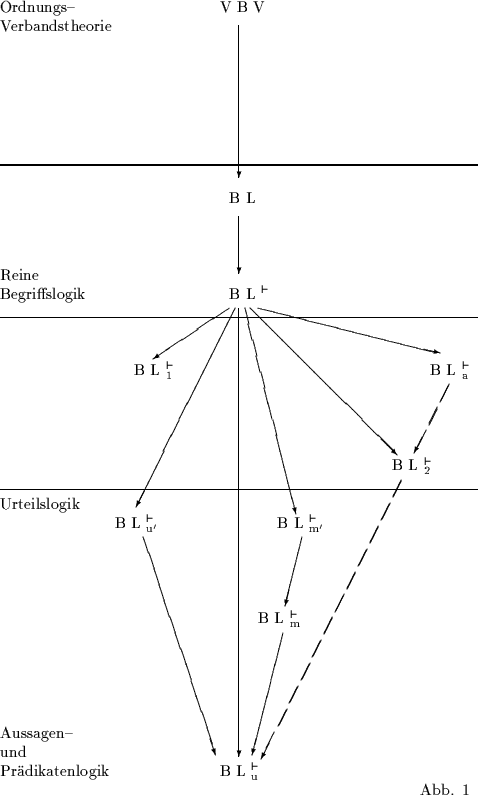
Wir werden im folgenden die einzelnen Kalküle kurz beschreiben und auch einige jeweils charakteristische Sätze angeben.
Der bisher gewonnene begriffslogische Kalkül BL zeigt noch einige Schwächen:
z.B. kann man die Regel
![]() ,
,
![]()
![]()
![]() hier nicht beweisen. Dieser Mangel wird behoben, indem man
axiomatisch einen Zusammenhang zwischen der Ableitbarkeitsbeziehung
hier nicht beweisen. Dieser Mangel wird behoben, indem man
axiomatisch einen Zusammenhang zwischen der Ableitbarkeitsbeziehung
![]() und der Kalkül-internen Beziehung
und der Kalkül-internen Beziehung ![]() herstellt:
Unter bestimmten Bedingungen soll es zu jedem Beweis
herstellt:
Unter bestimmten Bedingungen soll es zu jedem Beweis
|
|
Diese Forderung erinnert sehr an die Art und Weise, wie in den Gentzenschen ,,Kalkülen des natürlichen Schließens`` die Implikation ,,eingeführt`` wird und ebenso an das aus der Aussagenlogik bekannte sog. ,,Deduktions-Theorem``.
Es folgen die den neuen Kalkül BL![]() kennzeichnenden Axiome in
zweifacher Darstellung:
kennzeichnenden Axiome in
zweifacher Darstellung:
| BL |
|||
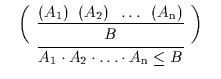 |
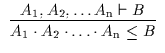 |
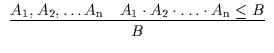 |
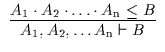
|
![]() a ist zu lesen als: Ist aus den Annahmen A
a ist zu lesen als: Ist aus den Annahmen A![]() bis
A
bis
A![]() die Formel B abgeleitet, so gewinnt man unter ,,Beseitigung``
dieser Annahmen (das deutet die Klammerung der A
die Formel B abgeleitet, so gewinnt man unter ,,Beseitigung``
dieser Annahmen (das deutet die Klammerung der A![]() bis A
bis A![]() an)
die nun im Kalkül ableitbare Formel A
an)
die nun im Kalkül ableitbare Formel A
![]() A
A
![]() ...
...
![]() A
A![]()
![]() B; oder anders: Aus dem Beweis A
B; oder anders: Aus dem Beweis A![]() ,
A
,
A![]() ,
...A
,
...A![]()
![]() B gewinnt man die Formel
A
B gewinnt man die Formel
A
![]() A
A
![]() ...
...![]() A
A![]()
![]() B.
B.
![]() b lautet auf Deutsch: Aus A
b lautet auf Deutsch: Aus A![]() ,
A
,
A![]() ,
...
A
,
...
A![]() sowie A
sowie A
![]() A
A
![]() ...
...
![]() A
A![]()
![]() B ist B ableitbar; oder: Aus der Formel
A
B ist B ableitbar; oder: Aus der Formel
A
![]() A
A
![]() ...
...![]() A
A![]()
![]() B
gewinnt man die Ableitung, den Beweis, die Regel A
B
gewinnt man die Ableitung, den Beweis, die Regel A![]() ,
A
,
A![]() ,
...A
,
...A![]()
![]() B.
B.
(Hierbei gelte die Einschränkung: Jede der Formeln A![]() bis
A
bis
A![]() sowie B sei von der Gestalt
sowie B sei von der Gestalt ![]() ,
,
![]() ,
,
![]() (für
(für
![]() ) oder
) oder ![]() (für
(für
![]() ).
).
Diese Einschränkung ist nur nötig, wenn man an der Unterscheidung von Urteils- und Begriffslogik unter dem Gesichtspunkt ,,Alle Verknüpfungszeichen sind Beziehungszeichen / Nicht alle Verknüpfungszeichen sind Beziehungszeichen`` interessiert ist; siehe Abschnitt 2.10 )
Tritt in einer der Prämissen A![]() bis A
bis A![]() die Variable (der
Index)
die Variable (der
Index) ![]() frei auf und wurde die Konklusion B unter Verwendung der
Variablen-Bedingung
frei auf und wurde die Konklusion B unter Verwendung der
Variablen-Bedingung ![]() NF... erschlossen, so ist dieses
NF... erschlossen, so ist dieses ![]() in der
Formel A
in der
Formel A
![]() A
A
![]() ...
...![]() A
A![]()
![]() B
durch
B
durch
![]() zu ,,binden``; z.B.:
zu ,,binden``; z.B.:
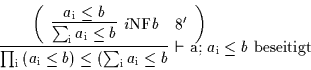
Fordert man für die Anwendung der Deduktionsregel ![]() a, daß Variablen
(Indizes) in A
a, daß Variablen
(Indizes) in A![]() bis A
bis A![]() und B nur nichtfrei auftreten
dürfen, dann sind Formeln wie
und B nur nichtfrei auftreten
dürfen, dann sind Formeln wie
![]()
![]()
![]() anscheinend erst in
BL
anscheinend erst in
BL
![]() (Abschnitt 3.4) beweisbar.
(Abschnitt 3.4) beweisbar.
Wie die neuen Regeln arbeiten, zeigt exemplarisch der folgende Beweis für
![]() ,
,
![]()
![]()
![]() :
:
| 1 | Grundregel 5 | |
| 2 | ( |
|
| 3 | ( |
nach Satz 1) aus 2 |
| 4 |
Die weiteren im Diagramm (Abb. 1) vorkommenden ,,Abkömmlinge`` von
BL![]() entstehen durch die Zusätze:
entstehen durch die Zusätze:
| BL |
0/1 | (bzw. |
|
| BL
|
m | ||
| BL
|
u | ||
| BL |
s |
Es soll erinnern
Zum Beweis etwa des für die Begriffe ![]() ,
,
![]() und
und ![]() im allgemeinen Sinne zu
lesenden Satzes
im allgemeinen Sinne zu
lesenden Satzes
![]() NF
NF![]()
![]()
![]()
![]()
![]() benötigt man das in der beschriebenen Weise
eingeschränkte Urteilsprinzip u'.
benötigt man das in der beschriebenen Weise
eingeschränkte Urteilsprinzip u'.
aufgefaßt werden.
Die Umkehrung gilt jedoch i.a. nicht: Die urteilslogisch beweisbare Formel
![]() ergibt z.B. verbandstheoretisch keinen Sinn.
ergibt z.B. verbandstheoretisch keinen Sinn.
| I1 | |
| I2 |
Kurz: Ein Individual-Begriff ist nicht widersprüchlich (0 heißt auch der
widersprüchliche Begriff, wegen ![]()
![]() in VBV) und
läßt sich nicht weiter in Unterarten aufteilen, spezialisieren. In den
Kalkülen VBV bis BL
in VBV) und
läßt sich nicht weiter in Unterarten aufteilen, spezialisieren. In den
Kalkülen VBV bis BL![]() braucht es keine Atome / Individual-Begriffe
(kurz: Individuen) zu geben.
braucht es keine Atome / Individual-Begriffe
(kurz: Individuen) zu geben.
Es folgt eine kleine Sammlung von nicht notwendigerweise unter dem Gesichtspunkt der ,,Wichtigkeit`` ausgewählten Sätzen, die aus den zuletzt eingeführten Axiomen beweisbar sind:
Für Individual-Begriffe gilt:
Satz 8) beleuchtet die Situation, in der eine materiale Implikation falsch ist: Vordersatz wahr, Hintersatz falsch.
Satz 7) bzw. 12) bildet den Hintergrund der sog. ,,Paradoxien der Materialen Implikation``: Von zwei Aussagen impliziert die eine die andere oder die andere die eine.
Satz 9) drückt eine bekannte Umformung der Implikation aus.
Die Sätze I1) und I2) drücken den Umstand aus, daß bei individuellem Subjekt jeweils universelles und partikuläres Urteil zusammenfallen. Dies könnte man als Auflösung der mittelalterlichen Streitfrage betrachten, ob die singulären Urteile zu den universellen oder zu den partikulären zu rechnen seien.