6. Andere Kalküldarstellungen

Unterabschnitte

• 6.1 Das Beispiel im Kalkül BL
• 6.2 Das Beispiel im Freytagschen Kalkül
• 6.3 Das Beispiel im Venn-Diagramm

Die bisher erwähnten Kalküle sind alle in einem bestimmten Sinne eindimensional, d.h. ihre Ausdrücke sind Zeichenreihen. Oft ist es aber lehrreich, ein und dasselbe Gebiet auf syntaktisch bzw. graphisch verschiedene Weise, gewissermaßen aus verschiedenen Perspektiven darzustellen. Man denke etwa an Freges ,,Begriffsschrift``, einen zweidimensionalen Kalkül, im Vergleich mit heutigen Formalismen. ,,Mehrsprachiges`` Arbeiten im genannten Sinne schützt davor, die Sache selbst mit einer ihrer Darstellungen zu verwechseln, und eröffnet die Möglichkeit, je nach Problemlage die jeweils geeignetere Symbolik einzusetzen, zumal die verschiedenen Darstellungen - wie man sich denken kann und wir gleich ansatzweise sehen werden - ihre je eigenen Vor- und Nachteile haben.

Aufgabe: Es sei der bereits oben (Abschnitt 2.6) angegebene Beweis für die Regel

  $a \leq b$, $c \leq d$  $\vdash$  $ac \leq bd$   zu finden.

6.1 Das Beispiel im Kalkül BL

Hier wird man am besten ,,rückwärts`` vorgehen und den Term  $bd$  in der Konklusion mit Regel 7 ,,aufspalten``:

$$\infer[7]{a \cdot c \leq b \cdot d}{a \cdot c \leq b & a \cdot c \leq d}$$

Da die so entstandenen Formeln weder Voraussetzungen noch Theoreme sind, muß man fortfahren und wird - wenn man keine bessere ,,Idee`` hat - versuchsweise jeweils eine Transitivitätsanwendung (Regel 5) ansetzen:

$$\infer[5]{a \cdot c \leq b}{a \cdot c \leq ~~ & ~~ \leq b}\hs... ...{2cm}\infer[5]{a \cdot c \leq d}{a \cdot c \leq ~~ & ~~ \leq d}$$

und dann die Zwischenterme geeignet wählen, was schließlich auf den vollständigen Beweis (siehe Abschnitt 2.6) führt.

6.2 Das Beispiel im Freytagschen Kalkül

Verwendet man dagegen einen mehrdimensionalen, auf v. Freytag Löringhoff zurückgehenden, stark an die sog. Semantische Netze erinnernden Kalkül, dann sieht obige Regel so
aus:

Vorausgesetzt seien unsere Regeln 5 und 7 in ,,wörtlicher`` Übersetzung (die Grundformeln 2 stecken bereits in der Gestalt des Operationszeichens):

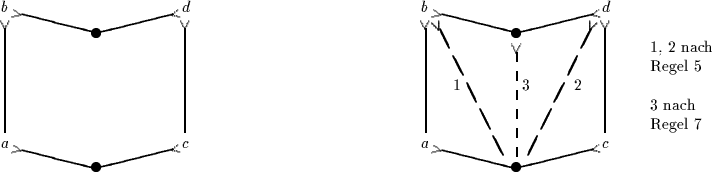
Hier liegt nun nahe (in diesem speziellen Falle; in anderen wird man - bei beiden Kalkülen - auf eine gemischte Rückwärts-Vorwärts-Strategie zurückgreifen), zunächst die Prämissen hinzuzeichnen und dann Schritt für Schritt neue Verbindungen herzustellen, bis sich die gewünschte Konklusion ergibt:

6.3 Das Beispiel im Venn-Diagramm

Anders beim Vennschen (Umfangs-) Diagramm: Nach Eintrag der Prämissen braucht man nur noch abzulesen, ob sich die gewünschte Konklusion ergibt (oder nicht), in unserem Falle, ob der zu   $ac$   gehörende Bereich ganz in dem zu   $bd$   gehörenden enthalten ist. Schraffur bedeutet Leerheit des betreffenden Bereiches.

Aber auch Beweise kann man mit den Angaben erstellen, die ein Venn-Diagramm liefert. Dabei werden auf einem vollkommen algorithmischen Wege von den zum Beweis der Konklusion nötigen Prämissen die unnötigen Teile abgespalten (die Prämissen werden spezialisiert), und die notwendigen Teile zur Konklusion zusammengefügt.

Für die Konklusion müssen die Felder    $a\overline{b}cd$,    $a\overline{b}c\overline{d}$, und    $abc\overline{d}$   gestrichen ($\leq 0$) sein, was durch die Prämissen erfüllt ist:

1	$a \leq b$	Prämisse
2	$c \leq d$	Prämisse
3	$a\overline{b} \leq 0$	aus 1	nach Regel 9
4	$c\overline{d} \leq 0$	aus 2	nach Regel 9
5	$a\overline{b}cd \leq 0$	aus 3	nach Regel 5 und Formel 2
6	$a\overline{b}c\overline{d} \leq 0$	aus 3	nach Regel 5 und Formel 2
7	$abc\overline{d} \leq 0$	aus 4	nach Regel 5 und Formel 2
8	$a\overline{b}c \leq 0$	aus 5 und 6	nach Satz 3)
9	$ac\overline{d} \leq 0$	aus 6 und 7	nach Satz 3)
10	$ac \leq b$	aus 8	nach Satz 2)
11	$ac \leq d$	aus 9	nach Satz 2)
12	$ac \leq bd$	aus 10 und 11	nach Regel 7