- ... Prämissen``1
- Vgl. [1,2],
[3, S. 131 ff], [4, S. 108 ff], [5, S. 49 ff].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 2
2
- Der Index K kann fehlen, wenn klar ist, um welchen Kalkül es
sich handelt, oder wenn von beliebigen Kalkülen die Rede ist.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... werden3
- Damit ist verträglich, daß eine
minimale Lösung
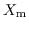 (siehe Abschnitte 4 und
5), aus der allein im allgemeinen Falle die Konklusion nicht
folgt, sich im besonderen als mit
(siehe Abschnitte 4 und
5), aus der allein im allgemeinen Falle die Konklusion nicht
folgt, sich im besonderen als mit  äquivalent erweist; womit sich zugleich
die Aufgabe stellt, notwendige und hinreichende Bedingungen dafür anzugeben,
daß dieser Fall eintritt.
äquivalent erweist; womit sich zugleich
die Aufgabe stellt, notwendige und hinreichende Bedingungen dafür anzugeben,
daß dieser Fall eintritt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... behandelt4
- Vgl. [3, S. 131 ff].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
zugrunde5
- Dieser unterscheidet sich von dem in [8, S. 28 ff,
S. 40 ff] verwendeten Kalkül BGS
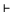 nur dadurch, das dessen
Axiom 2.4
nur dadurch, das dessen
Axiom 2.4

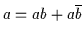 ,
,
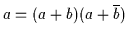 äquivalent durch die Regeln
äquivalent durch die Regeln 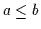
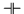
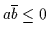 und
und
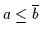
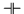
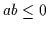 ersetzt ist.
ersetzt ist.
Wie man diesen Kalkül durch bestimmte Zusätze bis zur (vollen) Urteilslogik
BL
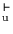 (äquivalent mit Aussagen- und Prädikatenlogik)
erweitert, wird in [8, S. 64 ff] gezeigt.
(äquivalent mit Aussagen- und Prädikatenlogik)
erweitert, wird in [8, S. 64 ff] gezeigt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Symbolik6
- Zur Äquivalenz
jeweils zugehöriger Kalküle vgl. [8, S. 32 ff].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
zugrundeliegt7
- Eine nach Peirce sog. ,,Abduktion``, vgl.
[3, S. 131].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Umfangsdiagramm8
- Man könnte ebensogut Inhaltsdiagramme
verwenden, vgl. [4, S. 64 ff].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
läßt9
- Unter Verwendung folgender Axiome für
,,
 ``:
``:
- 1)
 ,
,



 ,
,



- 2)
- Wenn


 und
und 

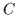 ,
dann
,
dann


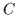 .
.
- 3)
- Wenn


 und
und 

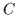 ,
dann
,
dann


 ,
,
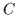 .
.
 ,
,
 ,
,
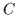 sind (eventuell leere) Systeme von Kalkül-Ausdrücken.
sind (eventuell leere) Systeme von Kalkül-Ausdrücken.
Die eine Richtung der zu beweisenden Äquivalenz erhält man ohne weiteres durch
Anwendung der Minimalitätsdefinition b) (,,Für alle 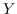 :
...``) auf
:
...``) auf
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
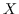 10
10
- Definiert man:

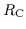
 genau wenn
genau wenn  ,
,
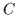

 und
und

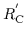
 genau wenn
genau wenn  ,
,
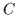

 und
und  ,
,
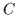

 ,
,
so wird 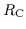 eine sog. Quasi-Ordnung und
eine sog. Quasi-Ordnung und
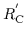 eine
Äquivalenzrelation.
eine
Äquivalenzrelation.
Ähnlich kann man auch BL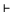 -intern definierien:
-intern definierien:
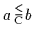
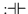
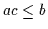 und
und
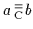
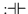
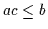 ,
,
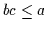 ;
es gilt dann:
;
es gilt dann:
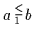
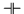
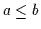 sowie
sowie
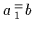
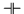
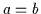 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Fälle11
- Da man im Kalkül
BL
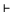 über Termnegation verfügt und daher alle syllogistischen
Relationen a, e, ..., ö ausdrücken kann, sind durch die Fälle 1 - 4
alle hier in Frage kommenden Möglichkeiten erschöpft.
über Termnegation verfügt und daher alle syllogistischen
Relationen a, e, ..., ö ausdrücken kann, sind durch die Fälle 1 - 4
alle hier in Frage kommenden Möglichkeiten erschöpft.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
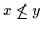 12
12
- Gleichungen und negierte Gleichungen brauchen nicht
gesondert behandelt werden, da sie sich in der Boole-Schröderschen Algebra
bzw. in der Begriffslogik bekanntlich auf jeweils äquivalente
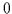 -(bzw.
-(bzw. 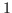 -)Subsumtionen bringen lassen:
-)Subsumtionen bringen lassen:
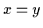
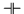
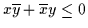
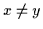
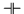
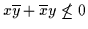
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
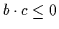 13
13
- Dies entspricht
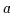 ë
ë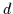 ,
,
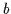 e
e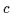 .
Da die Syllogistik im klassischen Sinne weder
.
Da die Syllogistik im klassischen Sinne weder 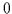 noch
noch 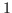 kennt, sollte man vielleicht lieber
kennt, sollte man vielleicht lieber
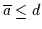 und
und
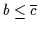 o.ä. schreiben. Wir bevorzugen i.a. die termnegationsfreie
Schreibweise oder eine solche, die den Zusammenhang von syllogistischer und
minimaler Lösung zu verdeutlichen geeignet erscheint.
o.ä. schreiben. Wir bevorzugen i.a. die termnegationsfreie
Schreibweise oder eine solche, die den Zusammenhang von syllogistischer und
minimaler Lösung zu verdeutlichen geeignet erscheint..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
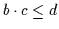 14
14
- Diese Lösung gilt auch schon für
distributive Verbände bzw. Begriffslogiken. Distributivität ist aber wohl
erforderlich, da man zum bequemen Nachweis der Lösungseigenschaft die sog. Schnittregel (vgl. [7]) zu benötigen scheint.
Die angegebene Lösung erledigt auch gleich den allgemeinen Fall mit n
Prämissen und m Konklusionen:
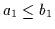 ,
...,
,
...,
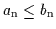 ,
,
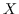

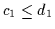 ,
...,
,
...,
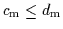 ,
da man Subsumtionen stets in äquivalente
,
da man Subsumtionen stets in äquivalente 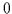 -Subsumtionen
umformen und diese dann in eine einzige zusammenfassen kann (Beweis mit
vollständiger Induktion).
-Subsumtionen
umformen und diese dann in eine einzige zusammenfassen kann (Beweis mit
vollständiger Induktion).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... geben15
- Abgesehen von der trivialen Lösung
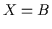 , hier also
, hier also
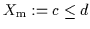 .
.
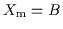 ist im Übrigen eine minimale Lösung für alle vier Fälle, hier allerdings
die einzig mögliche.
ist im Übrigen eine minimale Lösung für alle vier Fälle, hier allerdings
die einzig mögliche..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lassen16
- Vgl.
[8, S. 31 unten, S. 35 Theorem 16), dabei
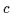 durch
durch 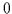 ersetzt,
S. 47 Theorem 21)].
ersetzt,
S. 47 Theorem 21)].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
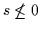 17
17
- Die Venn-Minimalität der Lösung ersieht man daraus, daß es
keine Möglichkeit gibt, zu den mit ,,-`` verbundenen Sternchen ein weiteres
hinzuzufügen und damit
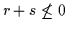 abzuschwächen, ohne damit
zugleich die Beweisbarkeit der Konklusion
abzuschwächen, ohne damit
zugleich die Beweisbarkeit der Konklusion 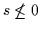 aufzugeben.
aufzugeben..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
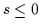 18
18
- Triviale Sonderlösung ist hier, wie schon oben angemerkt, die
Konklusion selbst, also
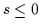 .
Diese Lösung ist auch Venn-minimal. Über
die Brauchbarkeit dieser Lösung kann man natürlich streiten.
.
Diese Lösung ist auch Venn-minimal. Über
die Brauchbarkeit dieser Lösung kann man natürlich streiten. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...-Theoremen19
- Vgl.
[8, S. 41 f].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
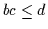 20
20
- Vgl. [8, S. 35 Theorem 16)].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
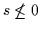 21
21
- Vgl. [8, S. 41 f].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Begriffslogik``22
- Vgl.
[8, S. 71 ff].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sind23
- Vgl. Fußnote 9).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zuzulassen24
- Schon in
BL
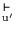 ist z.B.
ist z.B.
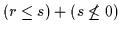 eine
minimale Lösung für den Fall 4' (siehe Abschnitt 5). Im
übrigen läßt sich jede Lösung
eine
minimale Lösung für den Fall 4' (siehe Abschnitt 5). Im
übrigen läßt sich jede Lösung 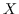 durch Addition der Konsequenz
durch Addition der Konsequenz  ,,zwangsminimalisieren``.
,,zwangsminimalisieren``.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... theoretischen25
- Man könnte sich z.B. fragen, unter welchen
Bedingungen die Transitivitätsregel
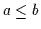 ,
,
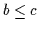

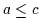 umkehrbar ist. Die Antwort besteht in der Minimallösung des
Rückschlußproblems:
umkehrbar ist. Die Antwort besteht in der Minimallösung des
Rückschlußproblems: 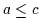 ,
,
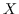

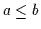 ,
,
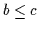 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ai26
- Vgl. [3, S. 142], [4, S. 108].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![]() (äquivalent mit Aussagen- und Prädikatenlogik)
erweitert, wird in [8, S. 64 ff] gezeigt.
(äquivalent mit Aussagen- und Prädikatenlogik)
erweitert, wird in [8, S. 64 ff] gezeigt.
 ,
,



 ,
,





 und
und 

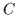 ,
dann
,
dann


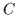 .
.


 und
und 

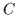 ,
dann
,
dann


 ,
,
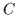 .
.
![]() ,
,
![]() ,
,
![]() sind (eventuell leere) Systeme von Kalkül-Ausdrücken.
sind (eventuell leere) Systeme von Kalkül-Ausdrücken.
![]() :
...``) auf
:
...``) auf
![]() .
.
![]()
![]()
![]() genau wenn
genau wenn ![]() ,
,
![]()
![]()
![]() und
und ![]() ,
,
![]()
![]()
![]() ,
,
![]() eine sog. Quasi-Ordnung und
eine sog. Quasi-Ordnung und
![]() eine
Äquivalenzrelation.
eine
Äquivalenzrelation.
![]() -intern definierien:
-intern definierien:
![]()
![]()
![]() und
und
![]()
![]()
![]() ,
,
![]() ;
es gilt dann:
;
es gilt dann:
![]()
![]()
![]() sowie
sowie
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
...,
,
...,
![]() ,
,
![]()
![]()
![]() ,
...,
,
...,
![]() ,
da man Subsumtionen stets in äquivalente
,
da man Subsumtionen stets in äquivalente ![]() -Subsumtionen
umformen und diese dann in eine einzige zusammenfassen kann (Beweis mit
vollständiger Induktion).
-Subsumtionen
umformen und diese dann in eine einzige zusammenfassen kann (Beweis mit
vollständiger Induktion).