| Alle |
Alle |
||
Gelegentlich begegnet man der Behauptung, aus gewissen Voraussetzungen folge logisch ein bestimmter Schlußsatz, muß dann aber feststellen, daß der beanspruchte Folgerungszusammenhang tatsächlich gar nicht besteht. So kann es einem etwa bei Diskussionen ergehen, bei der Prüfung juristischer Entscheidungsbegründungen, bei der Analyse scholastischer Argumentationen, aber auch bei dem Studium mathematischer Beweise.
Da man sich im Alltag - auch im wissenschaftlichen - fragmentarisch auszudrücken pflegt, also selbstverständlich erscheinende Voraussetzungen und Beweisschritte einfach wegläßt, gibt diese Beobachtung nicht unbedingt Anlaß zur Beunruhigung. Unter Umständen kann es jedoch interessant sein, einen solchen lückenhaften Gedankengang, ein sogenanntes Enthymem, zu einem vollständigen Beweis zu ergänzen, d.h. hier: weitere Voraussetzungen aufzusuchen, mit deren und der ursprünglichen Prämissen Hilfe die betreffende Konklusion dann tatsächlich beweisbar wird.
Dieses Vorgehen nennt man den ,,Rückschluß auf verborgene bzw. verschwiegene Prämissen``.
Dabei wird man sich nicht mit irgendeinem beliebigen System von Prämissen begnügen, die das Gewünschte leisten, sondern wird nach logisch möglichst schwachen Annahmen suchen, also solchen, die in einem gewissen Sinne ,,minimal`` sind. Zur Einführung diene ein Beispiel aus der Syllogistik, dem der Modus Barbara zugrundeliegt.
| Alle |
Alle |
||
Hier lautet eine naheliegende Lösung
![]() :
:
Nach (A6) gilt: ![]() ,
,
![]()
![]()
![]() .
Aber ist diese
Lösung irgendwie minimal ? Im Venn-Diagramm sieht das so aus:
.
Aber ist diese
Lösung irgendwie minimal ? Im Venn-Diagramm sieht das so aus:

Aus dem Diagramm entnimmt man ohne weiteres, daß die naheliegende
Beispiel-Lösung sozusagen zuviel liefert. Um ![]() aus
aus ![]() zu
gewinnen, genügt bereits folgende Schraffierung:
zu
gewinnen, genügt bereits folgende Schraffierung:

Die Lösung
![]() ist - wie auch aus dem Diagramm unmittelbar
ersichtlich - echt schwächer als die Beispiel-Lösung, denn aus
ist - wie auch aus dem Diagramm unmittelbar
ersichtlich - echt schwächer als die Beispiel-Lösung, denn aus ![]() folgt
folgt
![]() ,
aber nicht umgekehrt. Im anschaulichen, durch das
Venn-Diagramm gegebenen Sinne ist sie auch am schwächsten, denn für den Fall,
daß
,
aber nicht umgekehrt. Im anschaulichen, durch das
Venn-Diagramm gegebenen Sinne ist sie auch am schwächsten, denn für den Fall,
daß
![]() nicht, also
nicht, also
![]() gilt, ist
gilt, ist ![]() aus
aus ![]() nicht zu beweisen ( siehe Abb. 3 ).
nicht zu beweisen ( siehe Abb. 3 ).

Dies gilt nicht für die syllogistische Lösung ![]() ,
was man sich
ebenfalls leicht am Venn-Diagramm klar macht. Denn angenommen,
,
was man sich
ebenfalls leicht am Venn-Diagramm klar macht. Denn angenommen, ![]() gelte
nicht, also
gelte
nicht, also ![]() ,
so ist diese Lage immer noch mit
,
so ist diese Lage immer noch mit
![]() verträglich:
verträglich:
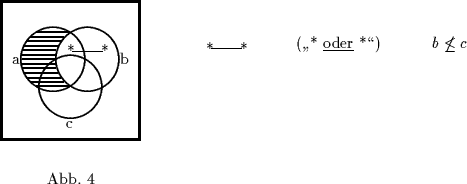
Als ,,Venn-minimal`` wollen wir im folgenden eine Lösung des Rückschlußproblems bezeichnen, die sich durch Betrachtung eines zugehörigen Venn-Diagramms als zur Gewinnung der Konklusion unerläßlich erweist.
Für eine universelle Konklusion gilt also: Venn-minimale Lösung des Rückschlußproblems ist die Menge der durch die Konklusion schraffierten Zellen ohne die Zellen, die durch die Prämissen schraffiert wurden.
Der Aufwand ist ![]() für
für ![]() als Anzahl der betroffenen Zellen.
als Anzahl der betroffenen Zellen.
Für partikuläre Konklusionen gilt: Für jede Sternsorte, die mindestens einen unschraffierten Stern unter den Zellen der Konklusion hat, ist eine minimale Lösung des Problems die Schraffur der noch unschraffierten außerhalb liegenden Sterne der jeweiligen Sternsorte.
Gibt es keine Sternsorte, die einen unschraffierten Stern unter den Zellen der Konklusion hat, so ist eine minimale Lösung des Rückschlußproblems die Einführung einer neuen Sternsorte, die alle Zellen der Konklusion abdeckt, und auch noch alle schraffierten Zellen (um möglichst schwach zu sein).
Schlimmstenfalls ist der Aufwand
![]() ,
also
,
also ![]() .
Zur Veranschaulichung betrachte man das Beispiel aus Abschnitt
3.3, das jeden der obigen Fälle enthält.
.
Zur Veranschaulichung betrachte man das Beispiel aus Abschnitt
3.3, das jeden der obigen Fälle enthält.
Im Rahmen der aristotelischen Syllogistik hat v. Freytag Löringhoff das Rückschlußproblem behandelt. Siehe dazu [4,5,6]. Die Ausgangslage ist hier:
Die Variablen ![]() ,
,
![]() ,
,
![]() ,
,
![]() stehen für beliebige Begriffsausdrücke;
stehen für beliebige Begriffsausdrücke;
![]() ,
,
![]() für beliebige der syllogistischen Relationen a,
e, i, o ( bzw. auch noch ä, ë, ï, ö, sofern man alle möglichen
(einfachen) Begriffsbeziehungen ins Spiel bringen, und keine Termnegation
benutzen will ). Die Lösung darf die Variablen höchstens negiert, aber
keine anderen Operationszeichen enthalten.
für beliebige der syllogistischen Relationen a,
e, i, o ( bzw. auch noch ä, ë, ï, ö, sofern man alle möglichen
(einfachen) Begriffsbeziehungen ins Spiel bringen, und keine Termnegation
benutzen will ). Die Lösung darf die Variablen höchstens negiert, aber
keine anderen Operationszeichen enthalten.
Man kann sich nun überlegen, wie man die jeweiligen Schlüsse in jedem der sich kombinatorisch ergebenden Fälle vervollständigen kann. Dabei sollen von Anfang an nur ,,syllogistisch minimale`` Lösungen in Betracht gezogen werden.
Die folgende Tabelle stellt ein Ergebnis dieser Bemühungen dar. Die Hypothese ist fett gezeichnet, die verborgenen Prämissen normal. Ein Bogen über zwei Begriffen bedeutet die Vertauschbarkeit beider Begriffe und damit eine weitere Lösung. Die Tabelle ist in vier Quadranten unterteilt, der vierte fehlt allerdings, da es hier keine Lösungen gibt.
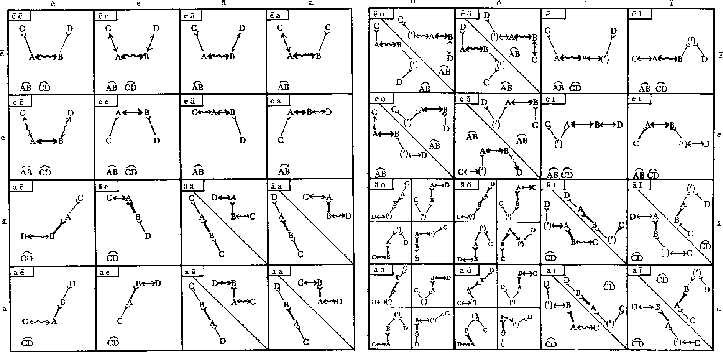
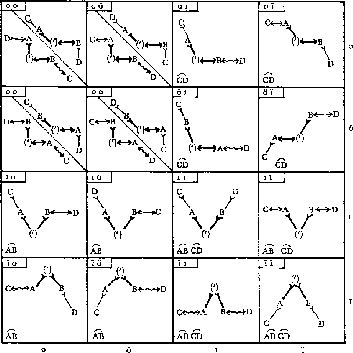
Die folgende Tabelle stellt noch einmal ausschließlich die Lösungen dar:
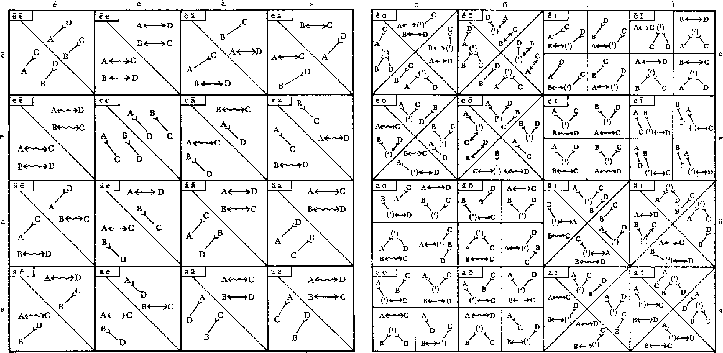
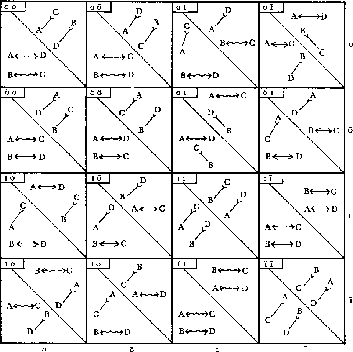
Die Tabellen stammen aus [6].
Fragen der Form
![]() ,
,
![]() ,
,
![]()
![]()
![]() bewirken bereits einen erheblichen Anstieg der
Lösungsmöglichkeiten, noch mehr Prämissen führen zu einem immer
stärkeren Anstieg der Zahl der Lösungsmöglichkeiten. Die Tabellen
würden bald Bücherregale füllen. Dieses Problem läßt sich aber mit Hilfe
eines Computerprogrammes recht einfach lösen. Dabei werden im Dialog mögliche
verborgene Prämissen akzeptiert oder verworfen, und so der Lösungsraum
erheblich eingeschränkt. Siehe dazu [6] und [7], welches
auch eine Programmdiskette enthält.
bewirken bereits einen erheblichen Anstieg der
Lösungsmöglichkeiten, noch mehr Prämissen führen zu einem immer
stärkeren Anstieg der Zahl der Lösungsmöglichkeiten. Die Tabellen
würden bald Bücherregale füllen. Dieses Problem läßt sich aber mit Hilfe
eines Computerprogrammes recht einfach lösen. Dabei werden im Dialog mögliche
verborgene Prämissen akzeptiert oder verworfen, und so der Lösungsraum
erheblich eingeschränkt. Siehe dazu [6] und [7], welches
auch eine Programmdiskette enthält.
Jemand sagt:
Weil alle Schlemmer Verschwender sind, sind einige Spiesser nicht zufrieden.
Aus welchen zusätzlichen Prämissen könnte dieser Mensch geschlossen haben, wenn er richtig geschlossen und nicht nur einfach so dahergeredet hat ? Die syllogistisch minimalen Lösungen sind, wie man aus den obigen Tabellen ablesen kann:
Kein Verschwender ist zufrieden
Alle Verschwender sind Spiesser
Alle zufrieden sind Spiesser
Nichts an Schlemmer ist an Spiesser
Die ersten beiden Lösungssysteme scheinen einigermaßen brauchbar, alle anderen sind ziemlich unsinnig. Die Venn-minimale Lösung ist dagegen:
Das sieht komplizierter aus als die syllogistisch minimale Lösung, ist aber exakt das, was als Prämisse fehlt. Jede beliebige, vielleicht schöner aussehende syllogistisch minimale Lösung hat mindestens die Venn-minimale Lösung zur Folge. Ein anderes Beispiel:
Jemand behauptet:
Weil alle Säugetiere Lebewesen sind, sind alle Affen braun, obwohl es Lebewesen gibt, die weder braun noch Säugetiere sind !
Auf welchen versteckten Prämissen könnte diese Behauptung beruhen ?
Die syllogistisch minimalen Lösungen sind (nach obigen Tabellen) die folgenden, wobei die angehängte partikuläre Bedingung aufgrund des starren Schemas überhaupt nicht mit betrachtet werden kann:
Alle Lebewesen sind braun
Nichts an Säugetiere ist an braun
Für dieses Beispiel erweisen sich die syllogistisch minimalen Lösungen als zu stark. Nicht nur das keines der beiden Lösungssysteme akzeptabel erscheint, sie widersprechen in jedem Fall auch der mit ,,obwohl`` angehängten zusätzlichen partikulären Prämisse. Die Venn-minimale Lösung ist:
Alle Lebewesen UND Affen sind braun
Diese Lösung widerspricht der partikulären Prämisse nicht. Das kann man einfach in einem Venn-Diagramm nachprüfen. Außerdem erscheint die Venn-minimale Lösung zumindest akzeptabler als die syllogistisch minimalen.
v. Freytag Löringhoffs Rückschluß ist relativ einfach anwendbar, sofern man die Tabellen verfügbar hat, oder aber in Besitz des Computerprogrammes dazu ist. Allerdings ist die Annahme, nämlich daß nur die in Prämissen und Hypothese vorkommenden Begriffe für die Lösung in Betracht gezogen werden sollen (und keine abgeleiteten), zu speziell. Die gebotenen Lösungen sind daher i.a. nicht ,,minimal`` bezogen auf Boolesche Verbände. D.h., kann man mindestens eine der angebotenen Lösungen akzeptieren, so kann man den Schluß geeignet vervollständigen, im anderen Fall weiß man nichts, weil die gebotenen Lösungen nicht zwingend erfüllt sein müssen. Dieser Umstand macht den syllogistisch minimalen Rückschluß für den eigentlich interessanten Fall praktisch wenig anwendbar.
Von Johann-Michael von Petzinger gibt es ein aus dem Jahr 1978 stammendes, bis heute leider unveröffentlichtes Papier [9] zur Theorie des allgemeinen minimalen Rückschlusses auf verborgene Prämissen. Die hier dargestellte Theorie, sowie die Einführung in die Rückschlußproblematik, sind im wesentlichen eine verkürzte und leicht modifizierte Version des eben erwähnten Artikels, welche im Rahmen einer langjährigen engen Zusammenarbeit mit dem obigen Autor entstanden ist.
Gegeben sei ein beliebiger Kalkül K sowie die Tatsache bzw. die Behauptung,
daß aus einem System von Kalkülausdrücken ![]() zusammen mit einem weiteren
solchen System
zusammen mit einem weiteren
solchen System ![]() ein anderes System von Ausdrücken
ein anderes System von Ausdrücken ![]() beweisbar ist; in
Zeichen:
beweisbar ist; in
Zeichen:
Im einfachsten Fall bestehen die Systeme ![]() und
und ![]() jeweils nur aus einem
einzigen Ausdruck.
jeweils nur aus einem
einzigen Ausdruck.
Hierbei seien ![]() und
und ![]() bekannt,
bekannt, ![]() sei ,,unbekannt`` und damit
,,gesucht``.
sei ,,unbekannt`` und damit
,,gesucht``. ![]() sollte - von trivialen Sonderfällen abgesehen - nicht aus
sollte - von trivialen Sonderfällen abgesehen - nicht aus
![]() alleine folgen, d.h. zur Ableitung von
alleine folgen, d.h. zur Ableitung von ![]() sollte
sollte ![]() i.a. tatsächlich mitbenutzt werden7.2.
i.a. tatsächlich mitbenutzt werden7.2.
Eine Möglichkeit bestünde darin, ,,minimal (schlechthin)`` eine Lösung zu
nennen, die relativ zum bekannten Prämissensystem ![]() bzgl. der
Ableitbarkeitsbeziehung ,,
bzgl. der
Ableitbarkeitsbeziehung ,,![]() `` schwächer ist als alle anderen Lösungen.
Wir definieren daher folgendermaßen:
`` schwächer ist als alle anderen Lösungen.
Wir definieren daher folgendermaßen:
(,,![]() ist aus
ist aus ![]() und
und ![]() im Kalkül K beweisbar``)
im Kalkül K beweisbar``)
Für alle ![]() :
Wenn
:
Wenn ![]() ,
,
![]()
![]()
![]() ,
dann
,
dann ![]() ,
,
![]()
![]()
![]() ,
,
![]() .
.
(,,Alle Lösungen ![]() haben zusammen mit
haben zusammen mit ![]() im Kalkül K
im Kalkül K ![]() und
und ![]() zur Folge``)
zur Folge``)
Die Bedingung aus Definition 7.2(b) ist vor dem Hintergrund von
Definition 7.2(a) äquivalent mit einer einfacher formulierten:
![]() ,
,
![]()
![]()
![]() .
.
Beweis: Der Äquivalenzbeweis gelingt unter Verwendung folgender Axiome
für ,,![]() ``, sowie einer quasi aussagen- und prädikatenlogischen
Einbettung:
``, sowie einer quasi aussagen- und prädikatenlogischen
Einbettung:
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() sind (eventuell leere) Systeme von Kalkül-Ausdrücken.
sind (eventuell leere) Systeme von Kalkül-Ausdrücken.
Die eine Richtung der zu beweisenden Äquivalenz erhält man ohne weiteres durch
Anwendung der Minimalitätsdefinition (,,Für alle ![]() :
...``) auf
:
...``) auf ![]() .
.
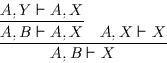
Die andere Richtung ist ebenfalls einfach: Sei ![]() eine beliebige Lösung.
eine beliebige Lösung.
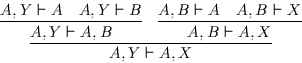
,,![]() ist minimale Lösung des Rückschlußproblems ( relativ zu
ist minimale Lösung des Rückschlußproblems ( relativ zu
![]() ,
,
![]() ,
K )``, genau dann wenn gilt:
,
K )``, genau dann wenn gilt: ![]() ,
,
![]()
![]()
![]() und
und
![]() ,
,
![]()
![]()
![]() ,
d.h. wenn
,
d.h. wenn ![]() Lösung und minimal ist.
Lösung und minimal ist.
Gibt es mehrere minimale Lösungen für ein Rückschlußproblem ![]() ,
so sind diese Lösungen vor dem Hintergrund des Prämissensystems
,
so sind diese Lösungen vor dem Hintergrund des Prämissensystems ![]() identisch.
identisch.
Beweis: Seien ![]() und
und ![]() zwei minimale Lösungen für ein
Rückschlußproblem
zwei minimale Lösungen für ein
Rückschlußproblem ![]() mit
mit ![]() oder
oder ![]() .
Dann gilt nach
Definition 7.3:
.
Dann gilt nach
Definition 7.3: ![]() ;
;
![]() ;
;
![]() und
und
![]() .
Es ist dann zu zeigen:
.
Es ist dann zu zeigen:
![]() .
.
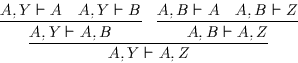
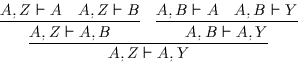
Wir betrachten nun die vier möglichen Fälle7.3, bei denen als bekannt
genau eine Prämisse und eine Konklusion der Gestalt ![]() oder
oder ![]() auftreten. Ebenso besitzen die syllogistischen Lösungen
(
auftreten. Ebenso besitzen die syllogistischen Lösungen
(
![]() ,
,
![]() etc. ) und die minimalen
(
etc. ) und die minimalen
( ![]() ) diese Gestalt und erfüllen die Bedingung, daß in
) diese Gestalt und erfüllen die Bedingung, daß in ![]() und
und ![]() kein Beziehungszeichen, also
kein Beziehungszeichen, also ![]() oder
oder ![]() ,
enthalten ist, sofern dies für
,
enthalten ist, sofern dies für
![]() ,
,
![]() ,
,
![]() ,
,
![]() gilt.
gilt.
| 1 | aa |
|
||
|
|
||||
| 2 | ao |
|
||
|
|
|
|||
|
|
||||
|
|
||||
|
|
||||
| 3 | oa | Hier scheint es keine Lösung zu geben7.6 . | ||
| 4 | oo |
|
||
|
|
|
|||
Da sich unverneinte wie verneinte Unterordnungen
![]() bzw.
bzw. ![]() jeweils in äquivalente
Null-Unterordnungen
jeweils in äquivalente
Null-Unterordnungen
![]() bzw.
bzw.
![]() umformen lassen, reduzieren sich die Fälle
1 - 4 auf folgende ( mit
umformen lassen, reduzieren sich die Fälle
1 - 4 auf folgende ( mit ![]() für
für
![]() und
und ![]() für
für
![]() ):
):
| 1' | |||
| 2' |
|
||
| 3' | |||
| 4' |
Ein Blick auf die zugehörigen Venn-Diagramme lehrt (Abb. 5-8a), daß die
Lösungen 1', 2' und 4' Venn-minimal sind, wobei allerdings die Lösung 4'
zuviel liefert:
![]() ,
an Stelle von
,
an Stelle von ![]() .
Lösung 4' ist jedoch nicht minimal im Sinne der Definition 7.3, da
.
Lösung 4' ist jedoch nicht minimal im Sinne der Definition 7.3, da
![]() ,
,
![]()
![]()
![]() nicht gilt.
nicht gilt.
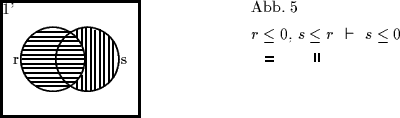

Die Venn-Minimalität der Lösung ersieht man daraus, daß es
keine Möglichkeit gibt, zu den mit ,,-`` verbundenen Sternchen ein weiteres
hinzuzufügen und damit
![]() abzuschwächen, ohne damit
zugleich die Beweisbarkeit der Konklusion
abzuschwächen, ohne damit
zugleich die Beweisbarkeit der Konklusion ![]() aufzugeben.
aufzugeben.

Triviale Sonderlösung ist hier, wie schon oben angemerkt, die
Konklusion selbst, also ![]() .
Diese ,,Lösung`` ist auch Venn-minimal.
Über die Brauchbarkeit dieser ,,Lösung`` kann man natürlich streiten.
.
Diese ,,Lösung`` ist auch Venn-minimal.
Über die Brauchbarkeit dieser ,,Lösung`` kann man natürlich streiten.
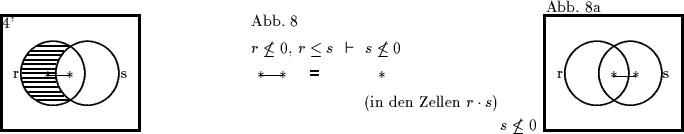
Die Minimalität der Lösungen für 1' und 2' sieht man so:
1': Zu zeigen ist ![]() ,
,
![]()
![]()
![]() ;
d.h.
;
d.h. ![]() ,
,
![]()
![]()
![]() .
Es gilt:
.
Es gilt:
Es gilt daher ![]()
![]()
![]() ;
also erst recht
;
also erst recht ![]() ,
,
![]()
![]()
![]() .
.
2': Auch hier gilt bereits ![]()
![]()
![]() ;
d.h.
;
d.h. ![]()
![]()
![]() ,
,
Hieraus folgt dann mit Kontraposition:
![]() .
.
Zur Lösung des Falles 1 (aa) kann man auf folgendem Wege gelangen:
|
|
|
|
| hieraus: |
|
|
| und dann: |
Die Lösung des vierten Falles (oo) kann auf die des ersten (aa) zurückgeführt werden:
| nach Satz 4.16 |
und weiter wie oben, oder aber
|
|
Kontraposition von Satz 4.5 | |
| nach 4' s.o. |
Auch der zweite Fall ao wird ähnlich behandelt:
|
|
nach 2' s.o. |
wobei man die Lösung 2' unmittelbar aus dem Venn-Diagramm oder aus der
BL![]() -Regel ( Satz )
-Regel ( Satz )
![]() ,
,
![]()
![]()
![]() entnehmen kann, die sich aus der Kontraposition
von Axiom A10 gewinnen läßt.
entnehmen kann, die sich aus der Kontraposition
von Axiom A10 gewinnen läßt.
v. Petzingers minimaler Rückschluß ist allgemeiner als der Venn-minimale Rückschluß, da er auf nahezu beliebige Kalküle bezogen ist, nicht nur auf Boolesche Verbände. Bei der Anwendung auf Boolesche Verbände, wie z.B. die Begriffslogik ergeben sich im wesentlichen die gleichen Ergebnisse, es gibt jedoch einen wichtigen Unterschied. Die Lösung im Fall 4 ist ,,Venn-minimal``, aber nicht ,,minimal``. Kontraponiert man dagegen, verwandelt den Fall 4 also in den Fall 1, so ist die Lösung von Fall 4 plötzlich doch minimal.
Der Grund ist: Die prinzipielle Funktionsmöglichkeit eines Schlusses ist z.B. in der Begriffslogik nicht gegeben, wenn man die Konklusion mit einer Prämisse tauscht (Das liegt in der Begriffslogik am Verhältnis von allgemeinen und partikulären Urteilen), wie dieses die Minimalitätsbedingung verlangt. Einzig erlaubte Vertauschungsoperation in der Begriffslogik ist die Kontraposition, bzw. die inkonsistente Triade.
Die Minimalitätsdefinition kann aber für Kalküle, die die Kontraposition
erlauben, z.B. so erweitert werden: ![]() ,
,
![]()
![]()
![]() oder
oder
![]() ,
,
![]()
![]()
![]() .
.