Welches ist nun eine geeignete Umsetzungsmethode eines Hyperdiagrammes für den Computer ? Dazu sehen wir uns das folgende Beispiel an:
Wir verwenden ein Venn-Diagramm für 3 Grundobjekte. Dieses hat 2![]() = 8
Zellen. Den drei Grundobjekten geben wir die Namen
= 8
Zellen. Den drei Grundobjekten geben wir die Namen ![]() ,
,
![]() und
und ![]() .
Eine
Zelle wird eindeutig definiert durch die Angabe, zu welchen Grundobjekten sie
gehört und zu welchen sie nicht gehört ( die Minterme ).
.
Eine
Zelle wird eindeutig definiert durch die Angabe, zu welchen Grundobjekten sie
gehört und zu welchen sie nicht gehört ( die Minterme ).
Desweiteren soll das Grundobjekt durch eine 1, sein Negat durch eine 0 gekennzeichnet werden. Das führt zu den folgenden Bezeichnungen der acht Zellen:
| 0 0 0 | 0 | |||||||
| 0 0 1 | 1 | |||||||
| 0 1 0 | 2 | |||||||
| 0 1 1 | 3 | |||||||
| 1 0 0 | 4 | |||||||
| 1 0 1 | 5 | |||||||
| 1 1 0 | 6 | |||||||
| 1 1 1 | 7 |
Für jede der Zellen ergibt sich in diesem Beispiel eine eindeutige Ziffernkombination als Identifikation. Wenn man die Ziffernkombinationen als dreistellige Dualzahlen betrachtet, ergeben sich die Zahlen von 0 bis 7.
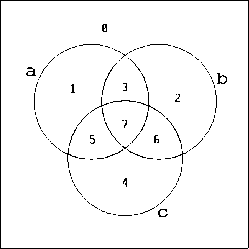
Nun werden wir die im Beispiel realisierte Idee verallgemeinern. Dazu ist eine Ordung der Grundobjekte notwendig. Diese kann beliebig sein, z.B. alphabetisch, muß dann aber fest sein.
Sei
![]() eine geordnete Folge von
eine geordnete Folge von ![]() Grundobjekten. Sei
Grundobjekten. Sei ![]() ein Minterm mit
ein Minterm mit ![]() Variablen, bestehend aus den Literalen
Variablen, bestehend aus den Literalen
![]() .
Sei
.
Sei ![]() das i-te Grundobjekt in der vorgegebenen Ordnung,
das i-te Grundobjekt in der vorgegebenen Ordnung,
![]() das Komplement des i-ten Grundobjekts. Es läßt sich eine charakteristische
Funktion
das Komplement des i-ten Grundobjekts. Es läßt sich eine charakteristische
Funktion ![]() wie folgt definieren:
wie folgt definieren:
Damit läßt sich eine Funktion ![]() definieren:
definieren:
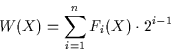
Die Funktionen ![]() und
und ![]() ordnen bei
ordnen bei ![]() Grundobjekten den Mintermen eindeutig
die Zahlen von 0 bis
Grundobjekten den Mintermen eindeutig
die Zahlen von 0 bis ![]() zu.
zu.
Beweis: Sei ![]() = 1. Dann gibt es zwei Minterme
= 1. Dann gibt es zwei Minterme ![]() und
und ![]() ,
die gemäß Definition 6.1 die Nummern 0 und 1 haben. Die Minterme
sind damit eindeutig durch die Zahlen 0 bis
,
die gemäß Definition 6.1 die Nummern 0 und 1 haben. Die Minterme
sind damit eindeutig durch die Zahlen 0 bis ![]() dargestellt.
dargestellt.
Seien nun bei ![]() Grundobjekten die
Grundobjekten die ![]() Minterme gemäß Definition
6.1 eindeutig durch die Zahlen von 0 bis
Minterme gemäß Definition
6.1 eindeutig durch die Zahlen von 0 bis ![]() dargestellt. Fügt
man nun ein weiteres Grundobjekt zu der dualen Zahlenfolge
dargestellt. Fügt
man nun ein weiteres Grundobjekt zu der dualen Zahlenfolge
![]() hinzu, so ergeben sich aus jeder Zahlenfolge zwei neue, nämlich
hinzu, so ergeben sich aus jeder Zahlenfolge zwei neue, nämlich
![]() und
und
![]() .
Es ist
.
Es ist
![]() =
=
![]() ,
die Zahl bleibt also erhalten. Es ist
,
die Zahl bleibt also erhalten. Es ist
![]() =
=
![]() ,
d.h. zu jeder Zahl wird
,
d.h. zu jeder Zahl wird ![]() hinzuaddiert. Es gibt also
keine ,,Kollisionen`` und auch keine ,,Lücke``, d.h.
hinzuaddiert. Es gibt also
keine ,,Kollisionen`` und auch keine ,,Lücke``, d.h. ![]() Grundobjekte sind
durch die Zahlen von 0 bis
Grundobjekte sind
durch die Zahlen von 0 bis ![]() eindeutig dargestellt.
eindeutig dargestellt.
Beweis: Unterscheiden sich zwei Minterme an mindestens einer Stelle
(dieses sei die Stelle ![]() ), so ist deren charakteristische Funktion
), so ist deren charakteristische Funktion
![]() an dieser Stelle entweder 0 oder
an dieser Stelle entweder 0 oder ![]() .
Aufgrund der binären
Konstruktion der Zahlen durch die Funktion
.
Aufgrund der binären
Konstruktion der Zahlen durch die Funktion ![]() läßt sich dieser fehlende
Summand nicht durch andere Summanden kompensieren, daher sind die Bildwerte der
Abbildung ebenfalls verschieden und die Abbildung ist injektiv. Da
läßt sich dieser fehlende
Summand nicht durch andere Summanden kompensieren, daher sind die Bildwerte der
Abbildung ebenfalls verschieden und die Abbildung ist injektiv. Da ![]() Minterme gemäß Satz 6.1 durch die Zahlen von 0 bis
Minterme gemäß Satz 6.1 durch die Zahlen von 0 bis ![]() dargestellt werden können, ist die Abbildung auch surjektiv, also bijektiv.
dargestellt werden können, ist die Abbildung auch surjektiv, also bijektiv.
Die Umkehrabbildung könnte z.B. wie folgt aussehen:
(mit ![]() als bitweisem ,,Booleschen`` UND-Operator)
als bitweisem ,,Booleschen`` UND-Operator)
Sei ![]() die Menge der Booleschen Funktionen eines Booleschen Verbandes mit
die Menge der Booleschen Funktionen eines Booleschen Verbandes mit
![]() Objekten. Sei
Objekten. Sei ![]() die Menge der Zellen eines Venn-Diagrammes,
welches aus einer unabhängigen Familie von
die Menge der Zellen eines Venn-Diagrammes,
welches aus einer unabhängigen Familie von ![]() Regionen gebildet wird. Sei
Regionen gebildet wird. Sei
![]() die Potenzmenge von
die Potenzmenge von ![]() .
Sei
.
Sei ![]() die Potenzmenge der Menge
die Potenzmenge der Menge
![]() .
Wir definieren eine Abbildung
.
Wir definieren eine Abbildung
![]() ,
die Boolesche Funktionen auf Mengen von Zahlen abbildet.
,
die Boolesche Funktionen auf Mengen von Zahlen abbildet.
Venn-Diagramme für ![]() Regionen und die Menge
Regionen und die Menge ![]() mit den Operatoren
mit den Operatoren
![]() ,
,
![]() und ' sind zueinander isomorph.
und ' sind zueinander isomorph.
Beweis: Satz 2.39 lieferte die Isomorphie zwischen Booleschen
Verbänden für ![]() Variablen und Venn-Diagrammen für
Variablen und Venn-Diagrammen für ![]() Regionen. Die
Abbildung
Regionen. Die
Abbildung ![]() ist eine isomorphe Abbildung (die Isomorphie basiert auf der
Bijektion zwischen Mintermen und den Zahlen aus Satz 6.2) zwischen
Booleschen Verbänden für
ist eine isomorphe Abbildung (die Isomorphie basiert auf der
Bijektion zwischen Mintermen und den Zahlen aus Satz 6.2) zwischen
Booleschen Verbänden für ![]() Variablen und der Menge
Variablen und der Menge ![]() .
Daher sind auch
Venn-Diagramme für
.
Daher sind auch
Venn-Diagramme für ![]() Regionen mit der Menge
Regionen mit der Menge ![]() isomorph.
isomorph.
Sei ![]() das
das ![]() -te Grundobjekt. Dann kann man die zugehörige Menge von
Zahlen auch durch die folgende Vorschrift gewinnen:
-te Grundobjekt. Dann kann man die zugehörige Menge von
Zahlen auch durch die folgende Vorschrift gewinnen:
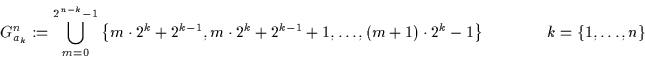
Aus der Menge der Zahlen von 0 bis ![]() werden die Zahlen ausgewählt, die
in dualer Darstellung an der
werden die Zahlen ausgewählt, die
in dualer Darstellung an der ![]() -ten Stelle eine 1 haben.
-ten Stelle eine 1 haben.
Für ![]() wechseln sich 0 und 1 jeweils ab (beginnend mit 0), die Länge der
0- und 1-Blöcke ist also 1. Für jedes weitere Grundobjekt verdoppelt sich die
Länge der 0- und der 1-Blöcke, die Länge ist allgemein
wechseln sich 0 und 1 jeweils ab (beginnend mit 0), die Länge der
0- und 1-Blöcke ist also 1. Für jedes weitere Grundobjekt verdoppelt sich die
Länge der 0- und der 1-Blöcke, die Länge ist allgemein ![]() .
Die Anzahl
der jeweiligen Blöcke halbiert sich bei jedem Schritt.
.
Die Anzahl
der jeweiligen Blöcke halbiert sich bei jedem Schritt.
Es seien ![]() und
und ![]() die zwei Booleschen Funktionen
die zwei Booleschen Funktionen ![]() und
und ![]() gemäß Definition 6.2 zugeordneten Mengen.
gemäß Definition 6.2 zugeordneten Mengen.
Man kann also ein Venn-Diagramm für ![]() Grundobjekte auf die Menge der Zahlen
Grundobjekte auf die Menge der Zahlen
![]() abbilden. Dabei ist jede Zahl eine
eindeutige Identifikation der jeweils gemeinten Zelle im Venn-Diagramm.
abbilden. Dabei ist jede Zahl eine
eindeutige Identifikation der jeweils gemeinten Zelle im Venn-Diagramm.
Ein Venn-Diagramm für ![]() Grundobjekte kann ganz einfach durch ein
eindimensionales Array oder eine lineare Liste mit
Grundobjekte kann ganz einfach durch ein
eindimensionales Array oder eine lineare Liste mit ![]() noch zu definierenden
Einträgen dargestellt werden, wobei die Einträge mit 0 beginnend fortlaufend
numeriert werden.
noch zu definierenden
Einträgen dargestellt werden, wobei die Einträge mit 0 beginnend fortlaufend
numeriert werden.
Jede Boolesche Funktion kann gemäß Satz 6.3 als eine einfache Menge
von Zahlen, als eine Teilmenge der Menge
![]() dargestellt werden. Hier ist eine Repräsentation als lineare Liste von Zahlen
am geeignetsten. Durch einen einfachen Parser werden die Prämissen/Konklusionen
gelesen und die Menge der betroffenen Zellen regelrecht ausgerechnet. Dazu sind
die ,,Booleschen`` Operationen UND, ODER und NICHT als Mengenoperationen
,,Schnitt``, ,,Vereinigung`` und ,,Komplementbildung`` auf den linearen Listen
realisiert.
dargestellt werden. Hier ist eine Repräsentation als lineare Liste von Zahlen
am geeignetsten. Durch einen einfachen Parser werden die Prämissen/Konklusionen
gelesen und die Menge der betroffenen Zellen regelrecht ausgerechnet. Dazu sind
die ,,Booleschen`` Operationen UND, ODER und NICHT als Mengenoperationen
,,Schnitt``, ,,Vereinigung`` und ,,Komplementbildung`` auf den linearen Listen
realisiert.
Das Grundobjekt ,,![]() `` wird im Programm also dargestellt durch eine Liste der
Zellennummern, die es im Venn-Diagramm belegt. Im obigen Beispiel für drei
Grundobjekte sind das alle die Nummern, die in der dualen Darstellung eine 1
ganz rechts haben, also die Zahlen 1, 3, 5 und 7. Das Grundobjekt ,,
`` wird im Programm also dargestellt durch eine Liste der
Zellennummern, die es im Venn-Diagramm belegt. Im obigen Beispiel für drei
Grundobjekte sind das alle die Nummern, die in der dualen Darstellung eine 1
ganz rechts haben, also die Zahlen 1, 3, 5 und 7. Das Grundobjekt ,,![]() `` des
Beispiels besteht aus den Zahlen 2, 3, 6 und 7. Das Objekt ,,
`` des
Beispiels besteht aus den Zahlen 2, 3, 6 und 7. Das Objekt ,,![]() UND
UND ![]() ``
entsteht dann als Schnittmenge der Listen der Grundobjekte ,,
``
entsteht dann als Schnittmenge der Listen der Grundobjekte ,,![]() `` und ,,
`` und ,,![]() ``;
es entspricht also einer Liste, welche die Nummern 3 und 7 enthält.
``;
es entspricht also einer Liste, welche die Nummern 3 und 7 enthält.