Individual- und Nicht-Individualbegriffe

Andreas Otte

01.09.1987¹

Die Logik unterscheidet Allgemeinbegriffe und Individualbegriffe. Ein Individualbegriff bezeichnet den Inhalt eines ganz bestimmten Gegenstandes und nur dieses einen Gegenstandes. Der Umfang eines Allgemeinbegriffes kann dagegen vieles enthalten.

Von Allgemeinbegriffen wird nur gefordert, daß sie meinbar sein müssen, und meinen kann man bekanntlich alles. Für Individuen gilt darüber hinaus noch, daß sie existieren und das sie unteilbar, also fertig, nicht mehr weiter spezifizierbar sind. Das ist ihre Individualität. Mehr interessiert im Rahmen der Logik nicht. Wir fragen nicht, was ein Individuum ist, bestenfalls in welchem Verhältnis es zu seiner Repräsentation (dem Individualbegriff) steht, sondern was man mit den Mitteln der reinen Logik über die Rolle der Individualbegriffe im Regelsystem der Logik aussagen kann.

Ein Begriff, der ein Individualbegriff ist, wollen wir mit einem I als Exponenten kennzeichnen, also z.B. als $a^{I}$. Das bedeutet nur, daß der Begriff $a$ als Individualbegriff behandelt werden soll. Der Inhalt des Begriffes wird durch die Rolle, die er durch das I zugewiesen bekommt, nicht verändert. Das ''Individualbegriffsein'' ist kein Inhalt des Begriffes selbst. Dieses Prädikat ergibt sich für uns aus dem Inhalt, ist aber kein Teil desselben.

Die Regelbezeichnungen stimmen größtenteils mit denen des Buches ''Neues System der Logik''[1] überein. Besonders aber bei den Nicht-Individualbegriffen sind Ergänzungen aus dem Artikel ''Zur Logik der Individualbegriffe''[2], aus meiner Diplomarbeit [3], sowie ein paar weitere eigene Überlegungen berücksichtigt, die zu einigen Veränderungen bei den Regelbezeichnungen führen, die das System übersichtlicher machen sollen. Andererseits wirkt das Regelsystem² an anderen Stellen durch Anlehnung an alte Bezeichnungen immer noch zu uneinheitlich. Am Ende dieses Artikels folgt deshalb ein Vorschlag für eine neue Systematik der Regelbezeichnungen.

Man kann auf die Individualbegriffe alle bisherigen Regeln anwenden, da sie natürlich auch meinbar sind; darüberhinaus gibt es aber noch Regeln, die den oben beschriebenen Charakteristiken der Individuen entsprechen. Diese Regeln wollen wir jetzt untersuchen. Danach beschäftigen wir uns noch mit dem Verhältnis zur Spezifikation und Generalisation, sowie mit der Negation von Individualbegriffen, bzw. mit der Negation der Eigenschaft ein Individualbegriff zu sein.

Ein Individuum existiert, kann also nicht widersprüchlich sein, der Begriff muß also echt über W (dem widersprüchlichen Begriff) stehen. Das drücken wir durch die folgende Operationsregel aus:

$\begin{xy} *!C\xybox{ (0,30)\OutText{6.1a}, (0,0)\OutBegriff{W}{W}, (20,20)... ...a^{I}}{A}, \ArtVon[@<1ex>]{W}{A} \KNichtGattungVon[@<-1ex>]{W}{A} } \end{xy}$

Desweiteren läßt sich ein Individuum nicht mehr unterteilen. Ein Individualbegriff darf also keine widerspruchsfreien, echten Arten haben. Zwischen ihn und W läßt sich keine Begriff mehr einschieben. Das ergibt das folgende Regelpaar, daß in ''Neues System der Logik'' als 6.21 und 6.22 bezeichnet wird. Abweichend von dieser Notation wollen wir die Regeln so bezeichnen:

$\begin{xy} *!C\xybox{ (0,50)\OutText{6.21a}, (0,0)\OutBegriff{W}{W1}, (20,2... ...W2}{B2} \ArtVon[@<1ex>]{B2}{A2} \NichtGattungVon[@<-1ex>]{B2}{A2} } \end{xy}$

Insofern sind Individualbegriffe, wenn sie in ''Begriffspyramiden'' auftauchen, immer die alleruntersten Begriffe.

Aus Regel 6.21a lassen sich zwei weitere Regeln für partikuläre Beziehungen ableiten:

$\begin{xy} *!C\xybox{ (0,80)\OutText{6.31a}, (40,65)\OutText{Beweis}, (40,6... ...{B2} \NichtDiversZu[@<1ex>]{RA2}{RB2} \KArtVon[@<-1ex>]{RA2}{RB2} } \end{xy}$

Wenn einige $a^{I}$ nicht $b$ sind, so folgt, daß alle $a^{I}$ nicht $b$ sind und einige $a^{I}$ $b$ sind, so folgt, daß alle $a^{I}$ $b$ sind.

Mit den obigen Regeln kann man beweisen, daß Individuen entweder total identisch oder divers zueinander sind:

$\begin{xy} *!C\xybox{ (0,40)\OutText{6.31}, (10,20)\OutText{Beweis}, (10,0)... ...ttungVon[@<-0.75ex>^{1.}]{A2}{B2} \KArtVon[@<-1.5ex>_{2.}]{A2}{B2} } \end{xy}$

Aus 6.31a folgt auch, daß für Individualbegriffe ein ''tertium non datur'', bzw. ein ''tendal'' unter schwächeren Bedingungen gilt. Für die Anwendung dieser Regeln muß nicht mehr gefordert werden, daß alle $a$ nicht $b$ sind, sondern es reicht bereits, daß einige $a$ nicht $b$ sind:

$\begin{xy} *!C\xybox{ (30,0)\OutText{2.~1.1}, (30,5)\OutText{1.~6.31a}, (10... ...A2} \KNichtDiversZu[@<-1ex>_{1.}]{B2}{A2} \KArtVon[_{2.}]{A2}{C2} } \end{xy}$

Damit sind wir bereits mitten in der Spezifikation und Generalisation. Das ''tendal'' mag als Beispiel gelten für noch ein paar andere ET- und VEL-Regeln, die bei Individualbegriffen schon unter schwächeren Bedingungen anwendbar werden.

Spezifiziert man einen Individualbegriff mit einem Allgemeinbegriff, und setzt probeweise jeweils eines der acht Urteile zwischen ihnen an, so ergeben sich drei relevante Begriffslagen, die Folgerungen zulassen. Alle anderen haben keine Auswirkungen oder führen auf eine der drei Möglichkeiten:

Einmal kann der Allgemeinbegriff zum Individualbegriff divers sein, und dann ist das Spezifikat = W (nach Regel 1.02b), oder der Individualbegriff hat an dem Allgemeinbegriff als Eigenschaft teil, und dann kommt nach Regel 1.01b der Begriff selbst heraus.

$\begin{xy} *!C\xybox{ (30,30)\OutText{Beweis}, (30,25)\OutText{1.~Ann.}, (3... ...pezifikat{C}{A} \Spezifikat{C}{B} \KGattungVon[@<1ex>^{2.}]{C}{A} } \end{xy}$

Oder der Individualbegriff ist Gattung des Allgemeinbegriffes und dann ist das Spezifikat mit dem Allgemeinbegriff total identisch (ebenfalls nach Regel 1.01b). Gibt es weitere Daten über das Verhältnis des Allgemeinbegriffes zum Individualbegriff könnten außerdem noch die Regeln 6.21a und 6.22a zum Zuge kommen.

Beim Spezifizieren zweier Individualbegriffe gibt es nur eine relevante Möglichkeit, nämlich, daß sie divers sind. Daraus folgt nach Regel 1.02b die Widersprüchlichkeit des Spezifikates:

$\begin{xy} *!C\xybox{ (30,30)\OutText{Beweis}, (30,25)\OutText{1.~Ann.}, (3... ...}{B}, \DiversZu[^{1.}]{A}{B} \Spezifikat{C}{A} \Spezifikat{C}{B} } \end{xy}$

Grundlegend neues hat sich nicht ergeben. Die Spezifikation erweist sich also als recht unfruchtbar im Zusammenhang mit Individualbegriffen.

Für das Generalisieren ist die Tatsache, daß einer der Ausgangsbegriffe ein Individualbegriff ist erst recht ohne Belang, denn keine der speziellen Operationsregeln für Individualbegriffe reicht nach oben über den Individualbegriff hinaus.

Generalisiert man dagegen zwei verschiedene Individualbegriffe, so geschieht etwas wichtiges. Das Generalisat ist auf jeden Fall kein Individualbegriff! Die Annahme es wäre doch einer, läßt sich mit Regel 6.21a zum Widerspruch füren:

$\begin{xy} *!C\xybox{ (65,35)\OutText{Beweis}, (65,30)\OutText{1.~Ann.}, (6... ...attungVon[@<1ex>^{2.}]{W}{A} \KNichtGattungVon[@<-1ex>_{3.}]{W}{B} } \end{xy}$

Diesen Sachverhalt stellen wir durch die folgende Regel dar:

$\begin{xy} *!C\xybox{ (10,20)\OutText{6.6a}, (22,17)\OutText{\ifmmode{I\hski... ...b^{I}}{B}, \DiversZu{A}{B} \Generalisat{C}{A} \Generalisat{C}{B} } \end{xy}$

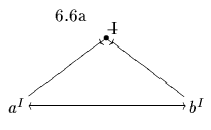
Einen solchen Begriff, und überhaupt alle, von denen wir wissen, daß sie keine Individuen bezeichnen, kennzeichnen wir mit einem durchstrichenen I-Exponenten, also so: $\ifmmode{I\hskip -7pt -} \else{\hbox{$I\hskip -7pt -$}}\fi$.

Wir stoßen jetzt in das weite Feld der Nicht-Individualbegriffe. Daß ''Nicht'' bedeutet, daß einem solchen Begriff der Status eines Individualbegriffes nicht zukommt. Der Inhalt des Begriffes wird durch dieses Prädikat, wie schon beim Individualbegriff, nicht verändert. Das ''Nicht'' beschreibt keine logische Negatbeziehung, obwohl man die Gesamtheit der Begriffe vollständig in Individual- und Nicht-Individualbegriffe aufteilen kann, denn es ist nicht auf Begriffsinhalte bezogen.

Auch für Nicht-Individualbegriffe gibt es spezielle Regeln:

Ist ein Individualbegriff Art eines Nicht-Individualbegriffes, so ist er immer eine echte Art, bei totaler Identität wäre der obere Begriff ebenfalls ein Individualbegriff.

$\begin{xy} *!C\xybox{ (30,20)\OutText{Beweis}, (30,15)\OutText{1.~Ann.}, (3... ...}}{B}, \ArtVon[@<1ex>^{1.}]{A}{B} \GattungVon[@<-1ex>_{2.}]{A}{B} } \end{xy}$

Deshalb muß eine widerspruchsfreie Möglichkeit dieser totalen Identität ausgeschlossen werden. Das drückt die Regel

$\begin{xy} *!C\xybox{ (5,25)\OutText{ZLI(4)a}, (0,0)\OutBegriff{a^{I}}{A}, ... ...\fi }}{B}, \ArtVon[@<1ex>]{A}{B} \KNichtGattungVon[@<-1ex>]{A}{B} } \end{xy}$

aus. Die Bezeichnung ZLI ist eine Abkürzung für den Artikel ''Zur Logik der Individualbegriffe''. Die nachfolgende in Klammern gesetzt Nummer ist die Nummer, die die Regel in dem Artikel innehatte. Das ''a'' ist wiederum eine eigene Erweiterung.

Ein Nicht-Individualbegriff ergibt sich auch, wenn man einen Individualbegriff negiert:

$\begin{xy} *!C\xybox{ (0,0)\OutBegriff{a^{I}}{A}, (20,0)\OutBegriff{b^{\ifmm... ...-$}}\fi }}{B}, \DiversZu[@<1ex>]{A}{B} \DisparatZu[@<-1ex>]{A}{B} } \end{xy}$

Diese Regel trägt in ''Zur Logik der Individualbegriffe'' die Nummer (11). Hier ist sie jedoch keine Regel. Die Totaldiversität erlaubt nämlich noch eine stärkere Folgerung. Ein Begriff, der zu einem Individualbegriff total divers ist, ist nicht nur ein Nicht-Individualbegriff, sondern er ist das Negat eines Individualbegriffes (damit natürlich auch ein Nicht-Individualbegriff). Die Regel dafür sieht so aus:

$\begin{xy} *!C\xybox{ (8,5)\OutText{6.7a}, (0,0)\OutBegriff{a^{I}}{A}, (20,... ...ne{a^{I}}}{B}, \DiversZu[@<1ex>]{A}{B} \DisparatZu[@<-1ex>]{A}{B} } \end{xy}$

Eine Ausnahme von dieser Regel ist eine ''Welt'' aus genau zwei, dann auch inhaltsfremden, Individuen.

Diese Regel und damit auch ihre Bezeichnung ist neu und fügt sich an die Regelbezeichnungen aus ''Neues System der Logik'' an.

Was ist nun das Negat eines Individualbegriffes? Ein Negat-Individualbegriff ist besonders inhaltsarm. Zwischen ihn und M (das Meinbare, der inhaltsleerste Begriff) kann kein Begriff mehr eingefügt werden. Sein Inhalt ist nicht mehr verkleinerbar, er liegt aber noch echt unter M. Das drückt die Regel

$\begin{xy} *!C\xybox{ (0,30)\OutText{6.1b}, (20,20)\OutBegriff{M}{M}, (0,0)... ...^{I}}}{A}, \ArtVon[@<1ex>]{A}{M} \KNichtGattungVon[@<-1ex>]{A}{M} } \end{xy}$

aus. Diese Regel ist offensichlich dual zur Regel 6.1a. Und so gelten überhaupt zu allen Regeln für Individualbegriffe entsprechende duale Regeln für Negat-Individualbegriffe. Hier die wichtigsten:

$\begin{xy} *!C\xybox{ (0,50)\OutText{6.21b}, (40,40)\OutBegriff{M}{M1}, (20... ...B2}{M2} \ArtVon[@<1ex>]{A2}{B2} \NichtGattungVon[@<-1ex>]{A2}{B2} } \end{xy}$

$\begin{xy} *!C\xybox{ (0,25)\OutText{6.31b}, (20,20)\OutBegriff{\overline{a^... ...1}{A1} \KArtVon[@<1ex>]{B2}{A2} \NichtDisparatZu[@<-1ex>]{B2}{A2} } \end{xy}$

Auch zu Regel 6.6a gibt es eine entsprechende duale Regel. Aber was für ein Begriff ist das Spezifikat aus zwei inhaltsfremden Negat-Individualbegriffen? Dieser Begriff ist ein Nicht-Negat-Individualbegriff, gekennzeichnet durch den Exponenten $\overline{\ifmmode{I\hskip -7pt -} \else{\hbox{$I\hskip -7pt -$}}\fi }$, also ein durchstrichenes, negiertes I. Das ''Nicht'' bedeutet hier, daß einem solchen Begriff der Status eines Negat-Individualbegriffes nicht zukommt, analog zu dem Verhältnis Individualbegriff - Nicht-Individualbegriff. ''Nicht'' und ''Negat'' sollte man hier sorgfältig unterscheiden.

$\begin{xy} *!C\xybox{ (7,20)\OutText{6.6b}, (12,0)\OutText{\overline{\ifmmod... ...egriff{C}, \Spezifikat{C}{A} \Spezifikat{C}{B} \DisparatZu{B}{A} } \end{xy}$

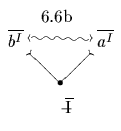
Die anderen Überlegungen zur Spezifikation und Generalisation bezüglich der Negat-Individualbegriffe brauchen wir hier nicht mehr durchzuführen, weil sich durch das Dualitätsprinzip die entsprechenden Rergebnisse für die Negate sehr schnell und einfach finden lassen.

Zur Regel ZLI(4)a gehört die Regel

$\begin{xy} *!C\xybox{ (5,25)\OutText{ZLI(4)b}, (20,20)\OutBegriff{\overline{... ...fi }}}{B}, \ArtVon[@<1ex>]{B}{A} \KNichtGattungVon[@<-1ex>]{B}{A} } \end{xy}$

, die nicht in ''Zur Logik der Individualbegriffe'' steht und nur aus Symmetriegründen so bezeichnet ist.

Für die Regel

$\begin{xy} *!C\xybox{ (8,5)\OutText{6.7b}, (0,0)\OutBegriff{\overline{a^{I}}... ...iff{a^{I}}{B}, \DiversZu[@<1ex>]{A}{B} \DisparatZu[@<-1ex>]{A}{B} } \end{xy}$

gibt es wieder eine Ausnahme, nämlich eine ''Welt'' aus genau zwei, dann auch umfangsfremden, Negaten von Individuen.

Genauso, wie man die ''Welt'' der Begriffe in Individual- und Nicht-Individualbegriffe teilen kann, so auch in Negat-Individualbegriffe und Nicht-Negat-Individualbegriffe. Der Bereich zwischen den Individualbegriffen und den Negat-Individualbegriffen ist dreigeteilt. Und zwar in die Generalisate aus Individualbegriffen, die Spezifikate von Negat-Individualbegriffen und schließlich die gewöhnlichen Allgemeinbegriffe.

Nun könnte man Nicht-Individualbegriffe und Nicht-Negat-Individualbegriffe auch logisch negieren, aber das Ergebnis ist aus den oben genannten Gründen nicht eindeutig. Deshalb lassen sich auch keine besonderen Regeln anwenden, wir brauchen uns um diese Begriffe nicht zu kümmern.

Wo liegt nun der Unterschied zwischen den gewöhnlichen Allgemeinbegriffen und den Generalisaten aus Individualbegriffen auf der einen Seite und den Spezifikaten aus Negat-Individualbegriffen auf der anderen Seite? Gemeinsam ist ihnen, das sie sowohl Nicht-Individualbegriffe als auch Nicht-Negat-Individualbegriffe sind. Den Unterschied erkennt man z.B., wenn man fragt, wie ein dritter, von den beiden definierenden verschiedener, Individualbegriff zu dem Generalisat steht. Er ist zu diesem divers, wie aus Regel 1.4a folgt:

$\begin{xy} *!C\xybox{ (25,20)\OutText{Beweis}, (25,15)\OutText{1.~Ann.}, (2... ...ersZu[_{1.}]{A}{D} \DiversZu[_{2.}]{B}{D} \KDiversZu[_{3.}]{D}{C} } \end{xy}$

Unter Generalisate aus Individualbegriffen können also nicht, wie es für gewöhnliche Allgemeinbegriffe charakteristisch ist, beliebig viele, auch noch gänzlich unbekannte Individuen fallen.

Der entsprechende duale Sachverhalt gilt auch für Spezifikate aus Negat-Individualbegriffen.

Ebensowenig, wie man durch immer weiteres spezifizieren vom Allgemeinbegriff zum Individualbegriff gelangt, denn gleichgültig, wie inhaltsreich man einen Allgemeinbegriff macht, lassen sich doch immer noch beliebig viele Begriffe meinen, auf die diese Eigenschaften zuträfen, so kommt man also durch Generalisieren vom Individualbegriff zum Allgemeinbegriff.

Das System der Begriffe läßt sich durch das folgende Diagramm darstellen:

Individualbegriffe	Nicht-Individualbegriffe
Nicht-Negat-Individualbegriffe				Negat-Individualbegriffe
	Generalisate aus Individualbegriffen	Allgemeinbegriffe	Spezifikate aus Negat-Individualbegriffen

Hier ist gut ersichtlich, daß einem Individualbegriff immer auch der Status eines Nicht-Negat-Individualbegriffes zukommt, ebenso, wie einem Negat-Individualbegriff immer auch der Status eines Nicht-Individualbegriffes. Umgekehrt gilt das natürlich nicht. Die folgenden Abschwächungen sind also erlaubt:

$\begin{xy} *!C\xybox{ (0,10)\OutText{6.8a}, (0,0)\OutText{I \Rightarrow \ove... ...arrow \ifmmode{I\hskip -7pt -} \else{\hbox{$I\hskip -7pt -$}}\fi } } \end{xy}$

Nun folgen noch Listen der Regelbezeichnungen im Vergleich zueinander:

Regelbezeichungen nach ''Neues System der Logik''	Regelbezeichnungen nach diesem Artikel	Regelbezeichnungen einer neuen Systematik
6.1a	6.1a	I.1a
6.21	6.21a	I.21a
6.22	6.22a	I.22a
	6.31a	I.31a
	6.32a	I.32a
6.31	6.31
6.32	6.32
6.4	6.4
6.5	6.5
6.6	6.6a	I.4a
	ZLI(4)a	I.5a
	6.7a	I.6a
	6.8a	I.7a
6.1b	6.1b	I.1b
	6.21b	I.21b
	6.22b	I.22b
	6.31b	I.31b
	6.32b	I.32b
	6.6b	I.4b
	ZLI(4)b	I.5b
	6.7b	I.6b
	6.8b	I.7b

In der neuen Regelsystematik sind die alten Regeln 6.31, 6.32, 6.4 und 6.5 herausgefallen, da es sich um einfachste Anwendungen der Regeln 6.31a bzw. 6.32a handelt, die nur Erwähnungscharakter haben sollten, aber keinen Regelcharakter.

Warum nicht sofort die neue Systematik?

Dieser Aufsatz kann nicht für sich stehen. Er ist gebunden an ''Neues System der Logik'' und auf dessen Regelbezeichnungen aufgebaut. Es muß deshalb einer Neuauflage von ''Neues System der Logik'' oder einen neuen Buch vorbehalten bleiben, diese neue oder eine ähnliche Regelsystematik einzuführen.