
Graphische Darstellungen zu logischen Problemen und Kategorien gibt es, seit es logische Untersuchungen gibt. Graphische Darstellungen logischer Beziehungen gab es offenbar erst viel später.
J.C. Lange veröffentlichte 1712 das Buch ,,Nucleus Logicae Weisianae``, das
nach dem Tode von Christian Weise dessen Logik behandelte. Die darin
vorkommenden logischen Diagramme sind aber wohl von Lange darin eingefügt
worden. Lambert, der Langes Werk studiert hat, sagt in seiner
,,Architectonic``, daß es eine gewisse Anzahl von durch Rechtecke und Kreise
illustrierte Syllogismen enthält. Langes Arbeiten blieben noch ohne große
Wirkung, erst mit Euler wurde die graphische Darstellung logischer Beziehungen
hoffähig. Lambert wie auch vor ihm Leibniz verwendeten waagerechte Striche, um
logische Beziehungen darstellen zu können. Diese Darstellungsform erwies sich
jedoch als ziemlich ungeeignet.
Die erste Veröffentlichung über die bekannten Euler Kreise findet sich in dem Werk ,,Briefe an eine deutsche Prinzessin``, Brief 102 - 108, der erste datiert vom 24. Februar 1761.
Euler repräsentierte eine Klasse durch einen Kreis und fragte sich, in welchen Relationen Inhalte und Umfänge zweier Klassen zueinander stehen können:

Dieses sind:
In Punkt 4 wird ein Problem der Euler-Diagramme sichtbar. Sie sind nicht eindeutig ! Es wurden zahlreiche Verbesserungsvorschläge gemacht, um diese Probleme zu beseitigen, als sonderlich effektiv erwies sich aber keiner. Ein anderes Problem ist, daß Widersprüche aus topologischen Gründen nicht gezeichnet werden können, schwierig wenn man gerade diese untersuchen will. Insgesamt waren die Euler-Diagramme aber doch insoweit brauchbar, daß sie sich in der Folgezeit weit verbreiteten.
Bereits in Schröders ,,Operationskreis des Logikkalkuls`` (1877) finden sich Diagramme für 2 bzw. 3 Begriffe, die den Venn-Diagrammen sehr ähnlich sind, jedoch nicht zum Eintragen von Beziehungen benutzt wurden. Auch Schröder schraffierte Zellen in seinen Diagrammen, allerdings nur um diese zu kennzeichen, wie wir das durch den Punkt getan haben.
1880 veröffentlichte John Venn seinen Artikel ,,On the diagrammatic and mechanical representations of propositions and reasoning`` [13], der als die eigentliche Geburtsstunde der Venn-Diagramme gelten muß. Bereits vorher hatte sich Venn mit graphischen Darstellungen logischer Beziehungen beschäftigt [11,12] und fühlte sich offenbar angeregt, die Funktionalität der bekannten Eulerschen Kreisdiagramme zu verbessern. Zusammen mit einigen anderen Artikeln veröffentlichte Venn seine Ergebnisse 1881 in dem Buch ,,Symbolic Logic`` [14]. Bemerkenswert an diesem Buch ist, daß Venn zu diesem Zeitpunkt noch an Booles ,,exklusivem Oder`` festhielt und daß die Venn-Diagramme noch keine Möglichkeit boten, partikuläre Urteile darzustellen und zu verarbeiten. 1894 veröffentlichte Venn die ,,Symbolic Logic`` [15] in zweiter Auflage mit einigen drastischen Änderungen. Zum einen verwendete er nun ebenfalls das ,,logische Oder``, zum anderen konnten nun auch partikuläre Urteile in den Diagrammen verarbeitet werden. Die Verwendung des ,,logischen Oders`` kam sicherlich durch den ,,Druck der Masse`` zustande, insbesondere durch Schröders ,,Vorlesungen zur Algebra der Logik``. Der Einbau der partikulären Urteile ergab sich offenbar durch die Bearbeitung und die Diskussion logischer Aufgaben, wie sie zu jener Zeit z.B. im ,,Mind`` in großer Zahl veröffentlicht wurden. Eine genaue Jahreszahl läßt sich nicht angeben, 1894 sind sie jedenfalls da. Allerdings markierte Venn die betroffenen Zellen nicht durch Sterne und verbindende Striche, sondern durch Zahlen. Die ,,Sternung`` geht auf die Schule von C.I. Lewis [16] zurück, und setzte sich sehr bald durch.
In der Folge regten die Venn-Diagramme zahlreiche weitere sehr ähnliche
graphische Darstellungen an. Genannt seien hier nur die Namen Lewis Carrol
(,,Alice im Wunderland``), Allan Marquand und Alexander Macfarlane. Die Zahl der Artikel, die sich mit der
Erweiterung von Venn-Diagrammen oder Venn-ähnlichen-Diagrammen für ![]() Objekte
beschäftigen, war und ist immer noch sehr groß.
Objekte
beschäftigen, war und ist immer noch sehr groß.
Freges graphischer Kalkül zur Urteilslogik blieb ohne großen Einfluß. Obwohl er die Urteilslogik neu inizierte, basierten die nachfolgenden Arbeiten fast nur auf linearen, algebraartigen Kalkülen.
Für die Begriffslogik entwarf Bruno v. Freytag Löringhoff in den 40er Jahren dieses Jahrhunderts einen zweidimensionalen, stark an Hasse-Diagramme oder an die heutigen semantischen Netze erinnernden Kalkül. Dabei bilden die Begriffe die Knoten, die verschiedenen Kantentypen stellen die logischen Beziehungen zwischen den Begriffen dar. Durch die Operationsregeln des Kalküls werden neue Kanten erzeugt. Unverbundene oder ,,nur wenig verbundene Knoten`` ( zwei Knoten können durch mehrere verschiedene Kanten in Beziehung zueinander stehen ) werden durch die Regeln des Kalküls miteinander verbunden und so die logischen Verhältnisse verdeutlicht.
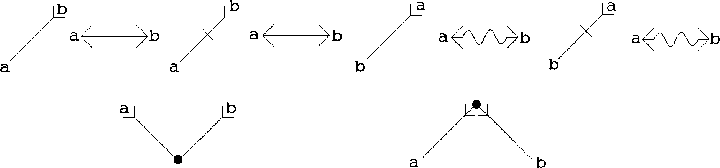
Da sind zunächst oben von links nach rechts die acht ,,aristotelischen`` Urteile.
Außerdem wird durch die in den Punkt einlaufenden Kanten die Spezifikation ![]() bzw. Generalisation
bzw. Generalisation ![]() dargestellt.
dargestellt.
Eine umfangreichere, wenn auch nicht sehr exakte und formale Einführung in diesen begriffslogischen Kalkül bieten die Bücher [4,5,6].
Ein großes Problem der Begriffslogik ist, daß es heute, wie schon im Abschnitt zur Geschichte der Logik zu lesen war, eine Geisteshaltung gibt, die formalisierte Logik automatisch mit Aussagen- und Prädikatenlogik gleichsetzt. Exakte Logik könne eben nur so und nicht anders aussehen.
Auch die Vorstellung einer Logik, die keine Werte hat, ist basierend auf dieser Geisteshaltung, mehr als ungewöhnlich. Der Abschnitt 4.2 zeigt dagegen sehr wohl, daß die Begriffslogik erstens formalisierbar ist, zweitens eine ganz gewöhnliche Basis hat (Boolescher Verband) und sich drittens ohne Probleme in eine Kalkülhierachie, welche die Aussagen- und Prädikatenlogik enthält, einordnen läßt.