Next: Über dieses Dokument ... Up: Artikel
BRUNO BARON VON FREYTAG LÖRINGHOFF. Logik I. Das
System der reinen Logik und ihr Verhältnis zur Logistik. Verlag
Kohlhammer, Stuttgart, ![]() 1972.
1972.
BRUNO BARON VON FREYTAG LÖRINGHOFF. Logik II. Definitionstheorie und Methodologie des Kalkülwechsels. Verlag Kohlhammer, Stuttgart, 1967.
BRUNO BARON VON FREYTAG LÖRINGHOFF UND JOHANN-MICHAEL VON PETZINGER. Zur Logik der Individualbegriffe. Zeitschrift für philosophische Forschung 28 (1974), Heft 3, 443-454.
BRUNO BARON VON FREYTAG LÖRINGHOFF. Neues System der Logik. Symbolisch-symmetrische Rekonstruktion und operative Anwendung des aristotelischen Ansatzes. Verlag Felix Meiner, Hamburg, 1985.
JOHANN-MICHAEL VON PETZINGER. Das Verhältnis von Begriffs- und Urteilslogik. Eine Untersuchung verschiedener Logikkalküle mit einem Exkurs über die Antinomien und den Intuitionismus. Dissertation, Universität Tübingen, 1975.
JOHANN-MICHAEL VON PETZINGER. Zum Rückschluß auf verborgene Prämissen. unveröffentlicht, 1978.
JOHANN-MICHAEL VON PETZINGER. Begriffslogik. unveröffentlicht, 1985.
Von jeher gilt Logik als eine Grunddisziplin der Philosophie, wie auch als Werkzeug wissenschaftlicher Arbeit überhaupt. Ihre Gesetze müssen in jeder Argumentation, die diesen Namen auch verdient, beachtet werden.
Es gibt heute zwei grundsätzliche Logikrichtungen:
Die Begriffslogik ist heutzutage gegenüber der Urteilslogik stark in den Hintergrund getreten. Ja, sie ist vielfach überhaupt unbekannt. Wer daher den heutigen Stand der Begriffslogik bewerten will, der muß zunächst die Geschichte der Begriffslogik, ja der Logik überhaupt betrachten. Die folgende Darstellung kann aber notgedrungen nur sehr kurz und demzufolge recht unvollständig sein.
Die Geschichte der Logik im Abendland als eigene Wissenschaft beginnt im Prinzip mit den später zum Organon zusammengefaßten logischen Schriften des Aristoteles.
Aristoteles betrieb im wesentlichen Begriffslogik, es finden sich jedoch auch einige modale und sogar urteilslogische Stellen in seinen Werken.
In der Scholastik wurde die Aristotelische Logik nahezu auf die Syllogistik und auf die Lehre vom hypothetischen Schluß reduziert, der syllogistische Bereich allerdings durch unnötigen Ballast erweitert (Kategorienlehre, Suppositionslehre, u.a.). Als solche wurde sie die klassische philosophische Logik, belastet mit allen möglichen psychologischen, linguistischen und ontologischen Einflüssen. Als Konsequenz dessen beschäftigten sich die mittelalterlichen Logiker mit lauter Problemen, die eigentlich nichts mit Logik zu tun hatten. Da war z.B. die Frage der Reihenfolge der Begriffe im i-Urteil, die Frage also, ob es einen Unterschied gibt zwischen: ,,Einige Pferde sind schwarz`` und ,,Einiges Schwarze ist Pferd``? Vom sprachlichen Standpunkt ist das sicherlich sehr interessant, aber rein logisch ist es ohne Bedeutung. Dennoch wurden Schlüsse eingeführt, die Rücksicht auf die Reihenfolge der Begriffe in den Urteilen nahmen, und machten die Logik damit komplizierter, als es eigentlich nötig gewesen wäre.
Auf der anderen Seite finden sich bei den Stoikern, bei Philon und im Mittelalter bei Ramon Lull bereits urteilslogische Ansätze. Im Grunde wurde allerdings nur Aussagenlogik betrieben, was eine zusätzliche eigene Begriffslehre nötig machte, da Begriffsbeziehungen in der Aussagenlogik nicht adäquat ausgedrückt werden können.
Mitte des 17. Jahrhunderts arbeitete Leibniz im wesentlichen begriffslogisch, wurde jedoch auch von Lull beeinflußt, und obwohl er sich eine ,,lingua universalis`` wünschte, hatte er doch keinen wirklich geeigneten Formalismus. Das ist der Grund für zahlreiche Fehler in den Leibnizschen Werken; Fehler, die später zu Unrecht dem Konzept ,,Begriffslogik`` angelastet wurden.
Begriffslogik und Urteilslogik liefen praktisch parallel nebeneinander her, wobei die Begriffslogik allerdings leichte Vorteile besaß. Bis zur Mitte des 19. Jahrhunderts gab es kaum bahnbrechende Entwicklungen in der Logik.
Das änderte sich mit Boole und De Morgan. Boole bahnte mit seiner Algebra der Logik neue Wege, indem er die Logik in einer von der Mathematik abgeleiteten formelartigen Weise darstellte. Booles Ansatz wurde von vielen weiterentwickelt und von Schröder nahezu vollendet.
Booles Ideen fanden Anwendung sowohl in der Begriffs- als auch in der Urteilslogik, jedoch führten sie zunächst nur in der Urteilslogik zum Ziel, die Begriffslogik blieb weiter unformalisiert. Schröder versuchte z.B. in späteren Jahren die Undurchführbarkeit einer ,,Inhaltslogik``, die weitgehend mit der Begriffslogik gleichgesetzt wurde, zu beweisen.
Frege leitete dann mit einem seiner wichtigsten Werke, das sinnigerweise den Namen Begriffsschrift trägt und nichts mit Begriffslogik zu tun hat, den Siegeszug der Urteilslogik ein. Obwohl Freges graphischer Kalkül heute nicht mehr benutzt wird, setzte sich sein Konzept ,,Das Urteil als Basis der Logik`` durch. Maßgeblich verantwortlich hierfür sind Russell und Whitehead mit ihren Principia Mathematica. Nur die Urteilslogik wurde ,,mathematisch`` formalisiert, die Begriffslogik aber blieb in den Händen der Philosophen und entwickelte sich nur unwesentlich weiter.
So kam es, daß die Begriffslogik sehr bald in den Ruf geriet, veraltet, probleminadäquat und unbrauchbar zu sein. Nicht etwa weil sie es wirklich war, sondern weil es unterlassen wurde, sie wie die Urteilslogik geeignet zu entwickeln und zu formalisieren.
Etwa 1938 begann dann Bruno Baron v. Freytag Löringhoff auch für die Begriffslogik den Weg der Formalisierung. Das war nicht das primäre Ziel v. Freytags, denn er wollte eigentlich nur der ,,philosophischen`` Begriffslogik ihre Bedeutung zurückgeben, um so ein Gegengewicht zu den ,,mathematischen`` Urteilslogiken zu schaffen.
Dazu mußten allerdings die Grundlagen der Begriffslogik genauer gefaßt werden, als es bis dahin geschehen war. Ausgehend von den Vorgaben seines philosophischen Lehrers Günther Jacoby und basierend auf dessen Logik-Vorlesung befreite v. Freytag die Begriffslogik zunächst von störenden psychologischen, ontologischen, linguistischen und gnoseologischen Einflüssen. Übrig blieb das Gerüst einer reinen Begriffslogik, die lediglich auf den beiden Begriffsbeziehungen ,,Identität`` und ,,Diversität`` beruhte, sowie auf der Möglichkeit, Begriffe als widerspruchsfrei zu deklarieren.
Eine kurze Darstellung:
Begriff ist, was ,,meinbar`` ist, also z.B.: ,,Hund``, ,,Geige``, ,,Streichinstrument``, ,,Sokrates``, ,,geflügeltes Einhorn`` und ,,viereckiger Kreis``.
Für diese reine Begriffslogik entwarf v. Freytag in den 40er Jahren einen zweidimensionalen, stark an Hasse-Diagramme oder an die heutigen semantischen Netze erinnernden Kalkül. Dabei bilden die Begriffe die Knoten, die verschiedenen Kantentypen stellen die logischen Beziehungen zwischen den Begriffen dar. Durch die Operationsregeln des Kalküls werden neue Kanten erzeugt. Unverbundene oder ,,nur wenig verbundene Knoten`` (zwei Knoten können durch mehrere verschiedene Kanten in Beziehung zueinander stehen) werden durch die Regeln des Kalküls miteinander verbunden und so die logischen Verhältnisse verdeutlicht.
Dieser Strichkalkül bietet einige didaktische Vorteile, wenn sich die Zahl der Begriffe in Grenzen hält, und eignet sich hervorragend zum Vorwärtsbeweisen. Ein kleines Beispiel wird dieses später verdeutlichen.
Unbeabsichtigt, wie schon oben bemerkt, entstand durch diesen Strichkalkül, der eigentlich nur als eine Art Hilfsnotation gedacht war, ein System von Grundformeln und -regeln. Auch wenn dieser Kalkül in keiner Weise ,,mathematisch`` aussah, war er doch ohne Zweifel eine Formalisierung der Begriffslogik. Der Strichkalkül wurde systematisch verbessert und als Mittel verwendet, auch den mathematik-abgeneigten Philosophen, die damals die Regel waren, einen gradlinigeren Zugang zur Anwendung der Logik zu liefern.
Mit Hilfe dieses Strichkalküls gelang es v. Freytag, die klassen- und urteilslogischen Einwände gegen die scholastische Syllogistik vom philosophisch-begriffslogischen Standpunkt aus gesehen zu klären, sowie die Syllogistik selbst zu straffen und von nicht-logischen Einflüssen zu befreien.
Der Rückschluß auf verborgene Prämissen hat deshalb so große Bedeutung, weil in den meisten Fällen Beweise nur Ethymen sind, d.h. verstümmelte Fragmente des eigentlichen Beweises. Triviale oder nur trivial erscheinende Prämissen werden oftmals unabsichtlich, manchmal aber auch mit Absicht weggelassen, um die ,,Lesbarkeit`` eines Beweises zu erhöhen. Diese verborgenen Prämissen zu finden, am besten noch die minimal notwendigen, kann gelegentlich recht interessante und überraschende Ergebnisse erbringen, denn unter Umständen kann man nichteinmal diese minimal notwendigen Prämissen zugeben, und dann bricht der Beweis zusammen.
Allerdings macht v. Freytags Ansatz recht starke Annahmen bezüglich der zu verwendenden Begriffe, so daß die Ergebnisse dieser Rückschlußtheorie für die minimale Ergänzung eines Schlusses nicht zwingend sind. Seine Rückschlußtheorie funktioniert daher nur im positiven Sinne; ist eines der vorgeschlagenen Prämissensysteme akzeptabel, so hat man eine Möglichkeit gefunden, den Beweis vervollständigen zu können.
Wie bereits oben bemerkt, eignet sich dieser graphische Kalkül sehr gut dazu, Beweise ,,vorwärts`` auszuführen. Es folgt ein kleines Beispiel, das einen Vorwärtsbeweis zeigen und zugleich einen kleinen Eindruck vom Strichkalkül geben soll. Es soll bewiesen werden, daß wenn ,,a`` Art von ,,b`` ist und ,,c`` Art von ,,d`` ist, dann auch ,,a und c`` Art von ,,b und d`` ist. Dabei sind ,,a``, ,,b``, ,,c`` und ,,d`` beliebige Begriffe.
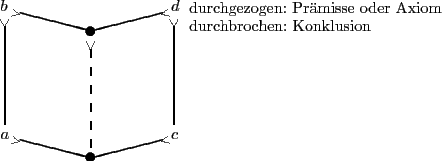
Der Strich mit den Schaftfedern gibt die Art-Gattungsbeziehung an, wobei die Gattung am Ende mit den Schaftfedern sitzt. Der Punkt in den zwei Art-Gattungsbeziehungen einlaufen, kennzeichnet das Spezifikat, also die Und-Verknüpfung zweier Begriffe. Die folgenden beiden Regeln werden für den Beweis benötigt: Das ,,dictum de omni`` (Transitivität) und die das Spezifikat quasi definierende Regel, nämlich daß das Spezifikat zweier Begriffe die allgemeinste Art der beiden Begriffe ist.
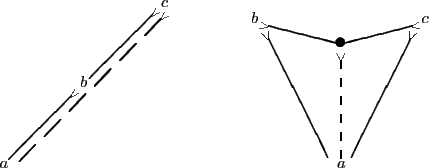
Zum Beweis geht man wie folgt vor: man zeichnet zunächst die Prämissen hin und stellt dann Schritt für Schritt neue Verbindungen her, bis sich die gewünschte Konklusion ergibt. Das ist das typische Vorgehen in einem Vorwärtsbeweis.
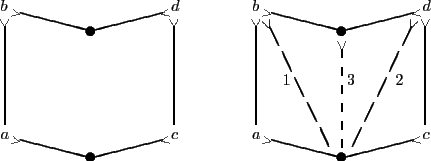
1 und 2 sind dabei Transitivitätsanwendungen, 3 wendet die Spezifikatregel an.
Auf dieser Grundlage entwickelte Johann-Michael v. Petzinger, ein Schüler v. Freytags, begriffslogische Kalküle, die in ihrer Erscheinungsform sehr den urteilslogischen ,,mathematischen`` Kalkülen ähnelten. An diesen Kalkülen trat sehr deutlich die verbandstheoretische Struktur der Begriffslogik zutage. Gedacht waren diese ,,mathematischen`` Begriffslogikkalküle zunächst nur für den Vergleich von Begriffs- und Urteilslogik; es stellte sich jedoch heraus, daß diese Kalküle besonders gut für die Technik des Rückwärtsbeweisens geeignet waren. Auch dieses wird später an einem Beispiel verdeutlicht werden.
In diesen Kalkülen bedeutet ![]() das Art-Gattungs-Verhältnis,
das Art-Gattungs-Verhältnis, ![]() die totale Identität, Überstreichen kennzeichnet die Negation,
die totale Identität, Überstreichen kennzeichnet die Negation, ![]() bzw.
bzw. ![]() bezeichnet die Generalisation (oder),
bezeichnet die Generalisation (oder), ![]() bzw.
bzw. ![]() die
Spezifikation (und), der waagerechte Strich kennzeichnet das
Ableitungsverhältnis.
die
Spezifikation (und), der waagerechte Strich kennzeichnet das
Ableitungsverhältnis.
Eine Axiomatik der Begriffslogik im Petzingerschen Sinne könnte etwa so aussehen (andere Axiomatisierungen sind möglich):
| A1 | |
A6 |
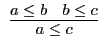 |
|||||
| A2a |
|
A7 |
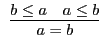 |
|||||
| A2b |
|
|||||||
| A3a | |
A8a |
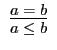 |
A8b |
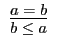 |
||
| A3b | |
||||||
| A4a | |
A9 |
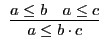 |
|||||
| A4b | |
|||||||
| A5a |
|
A10 |
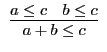 |
|||||
| A5b |
|
| A2' |
|
A9' |
![$\begin{array}{c}\infer[i{\rm NF}a]{a
\leq \prod_{i}{b_{i}}}{a \leq b_{i}}\end{array}$](img27.gif) |
|||||
| A3' |
|
A10' |
![$\begin{array}{c}\infer[i{\rm
NF}b]{\sum_{i}{a_{i}} \leq b}{a_{i} \leq b}\end{array}$](img29.gif)
|
Die beiden folgenden, in zweifacher Darstellung gegebenen Regeln stellen eine
Beziehung zwischen dem Art-Gattungs-Verhältnis (der Identitätsbeziehung)
![]() und der Ableitungsbeziehung
und der Ableitungsbeziehung ![]() (bisher durch den waagerechten
Strich symbolisiert) her:
(bisher durch den waagerechten
Strich symbolisiert) her:
| A11 |
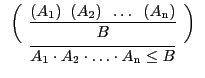 |
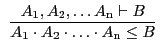 |
|
| A12 |
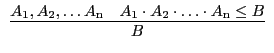 |
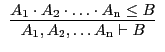
|
Desweiteren gibt es auch noch einen Kalkül, der die Bedeutung von ,,![]() kommt
nicht frei in ... vor`` (
kommt
nicht frei in ... vor`` (![]() NF
NF![]() ) festlegt. Das soll hier aber
entfallen.
) festlegt. Das soll hier aber
entfallen.
Die Axiome sind wie folgt zu verstehen:
Andererseits kann man den Begriff ,,a`` auch beschreiben als Und-Verknüpfung der ,,a oder b`` mit den ,,a oder Nicht-b,,.
Für das Alphabet dieses im folgenden BL![]() genannten Kalküls gilt:
genannten Kalküls gilt:
Die eindeutige Lesbarkeit der Ausdrücke wird nötigenfalls durch Setzen von Klammern gewährleistet.
Typisch für logische Kalküle ist, daß alle Formeln auch Terme sind, bzw. daß alle Beziehungszeichen auch wie Verknüpfungszeichen behandelt werden dürfen. Dies liegt daran, daß in der Logik die Beziehung von Grundobjekten wiederum ein Grundobjekt ist, d.h. die Beziehung von Begriffen ist wieder ein Begriff, die Beziehung von Urteilen ist wieder ein Urteil.
Zumindest für die Begriffslogik der 1. Ebene scheint es unsinnig, zuzulassen,
daß auch alle Verknüpfungszeichen wie Beziehungszeichen behandelt werden
dürfen, denn ein Allgemeinbegriff als alleinstehender Term in einer Ableitung
macht wenig Sinn (keine Wertigkeit). Auf höherer Ebene, wenn auch
beliebigstellige Relationen und Funktionen als Begriffe aufgefasst werden, macht
es allerdings Sinn, so daß diese Auffassung von Verknüpfungszeichen für die
Begriffslogik nicht ausgeschlossen werden darf. Ausgedrückt würde das durch
die Regel: ,,Behandle jeden Term ab der zweiten Ebene wie eine Formel``. Auf
höherer Ebene können dann auch ![]() und
und ![]() als
Beziehungszeichen, sowie das Komma als Verknüpfungszeichen aufgefaßt werden.
als
Beziehungszeichen, sowie das Komma als Verknüpfungszeichen aufgefaßt werden.
Dieser Kalkül eignet sich, wie bereits bemerkt, sehr gut zum rückwärts beweisen, d.h. ausgehend von der Konklusion versucht man den Beweis rückwärts zu entwickeln, um so schließlich Voraussetzungen und/oder Grundformeln zu erreichen.
Der Beweis des Satzes, der bereits bei v. Freytags Kalkül als Beispiel gebracht
wurde, gestaltet sich hier wie folgt. In der Konklusion
![]() wird zunächst der Term
wird zunächst der Term ![]() mit Regel A9 ,,aufgespalten``:
mit Regel A9 ,,aufgespalten``:
Da die so entstandenen Formeln weder Voraussetzungen noch Theoreme sind, muß man fortfahren und wird - wenn man keine bessere ,,Idee`` hat - versuchsweise jeweils eine Transitivitätsanwendung (Regel A6) ansetzen,
und dann die Zwischenterme geeignet wählen, was schließlich auf den vollständigen Beweis führt:
![\begin{displaymath}
\infer
[A9]
{a \cdot c \leq b \cdot d}
{\infer
[A6]
{a ...
...\leq d}
{\deduce
[A2]
{a \cdot c \leq c}
{}
&
c \leq d}}
\end{displaymath}](img121.gif)
Den Kalkül BL![]() kann man verstärken:
kann man verstärken:
Dieses zusätzliche Axiom hat im Zusammenhang mit der Negation die Zweiwertigkeit (Urteile sind entweder wahr oder falsch) der Urteilslogik vom Frege-Typ zur Folge.
Läßt man die Quantoren-Axiome A2', A3', A9' und A10' weg, so bekommt man durch Hinzufügung des Urteilsprinzips einen Kalkül, der der Aussagenlogik äquivalent ist.
Typisch für die Urteilslogik ist im übrigen, daß alle Terme auch Formeln sind, also daß alle Verknüpfungszeichen wie Beziehungszeichen behandelt werden dürfen.
Ähnlich wie Begriffe kann man auch Kalküle miteinander vergleichen. Insbesondere das Verhältnis der Über- und Unterordnung ist von Bedeutung. Es läßt sich u.a. folgendermaßen definieren (wobei zunächst der Fall betrachtet wird, daß die beiden Kalküle dasselbe Vokabular besitzen):
Der Kalkül K![]() heißt stärker/spezieller als der Kalkül
K
heißt stärker/spezieller als der Kalkül
K![]() , wenn
, wenn
Zwei Kalküle heißen äquivalent/gleichwertig, wenn jeweils der eine stärker als der andere ist.
Unterscheiden sich zwei zu vergleichende Kalküle im Vokabular, so wird eine ,,Übersetzung`` benötigt, die in einem bestimmten Sinne eindeutig sein muß, um gewisse Entartungsfälle auszuschließen2, und obige Definitionen müssen sinngemäß geändert werden.
Das wichtigste Ergebnis des mit den oben beschriebenen Mitteln durchgeführten Kalkülvergleiches zwischen Begriffs- und Urteilslogik war die Erkenntnis, daß Begriffslogik und Urteilslogik nicht etwa grundsätzlich verschieden sind, wie man es erwarten könnte, sondern daß die Urteilslogik eine spezielle Begriffslogik ist, d.h. also neben den urteilslogisch gedeuteten begriffslogischen Axiomen noch über ein zusätzliches, speziell urteilslogisches, Axiom verfügt.
Gemäß der Inhalts-Umfangs-Relation bewirkt ein größerer Inhalt (eine
stärkere Axiomatik) einen kleineren Umfang, d.h. die Urteilslogik ist nicht
mehr so allgemein deutbar wie die schwächere Begriffslogik. In der üblichen
Urteilslogik sind z.B. Ausdrücke wie ![]() oder
oder ![]() mit
mit ![]() bzw.
bzw. ![]() äquivalent.
äquivalent.
Außerdem wurde die Theorie des Rückschlusses auf verborgene Prämissen auf Begriffsverknüpfungen erweitert, und im Prinzip unabhängig vom Objektkalkül gemacht. In dieser Form ist der Rückschluß auf verborgene Prämissen hervorragend geeignet, die oft unvollständig aufgeschriebenen Argumentationen in beliebigen Kalkülen auf ihre verborgenen Voraussetzungen hin zu untersuchen.
Etwas technischer ausgedrückt: Gegeben sei ein beliebiger Kalkül K (eine
kalkülisierte bzw. formalisierte Theorie o.ä.) sowie die Tatsache, daß aus
einem System von Kalkülausdrücken ![]() zusammen mit einem weiteren solchen
System
zusammen mit einem weiteren solchen
System ![]() ein anderes System von Ausdrücken
ein anderes System von Ausdrücken ![]() beweisbar ist; in Zeichen:
beweisbar ist; in Zeichen:
Im einfachsten Fall vertreten ![]() und
und ![]() jeweils einen einzigen Ausdruck.
jeweils einen einzigen Ausdruck.
Hierbei seien ![]() und
und ![]() bekannt,
bekannt, ![]() sei ,,unbekannt`` und damit
,,gesucht``.
sei ,,unbekannt`` und damit
,,gesucht``. ![]() sollte - von trivialen Sonderfällen abgesehen - nicht aus
sollte - von trivialen Sonderfällen abgesehen - nicht aus
![]() alleine folgen, d.h. zur Ableitung von
alleine folgen, d.h. zur Ableitung von ![]() sollte
sollte ![]() im allgemeinen
tatsächlich mitbenutzt werden.
im allgemeinen
tatsächlich mitbenutzt werden.
v. Petzinger definiert:
(,,![]() ist aus
ist aus ![]() und
und ![]() im Kalkül K beweisbar``)
im Kalkül K beweisbar``)
Für alle ![]() : Wenn
: Wenn ![]() ,
, ![]()
![]()
![]() , dann
, dann ![]() ,
,
![]()
![]()
![]() ,
, ![]() .
.
(,, Alle Lösungen ![]() haben zusammen mit
haben zusammen mit ![]() im Kalkül K die Ausdrücke
im Kalkül K die Ausdrücke ![]() und
und ![]() zur Folge``)
zur Folge``)
Man kann zeigen, das diese Minimalitätsbedingung äquivalent ist mit der
folgenden wesentlich einfacheren: ,,![]() ist eine minimale Lösung
des Rückschlußproblems (relativ zu
ist eine minimale Lösung
des Rückschlußproblems (relativ zu ![]() ,
, ![]() , K)``, genau wenn gilt:
, K)``, genau wenn gilt: ![]() ,
,
![]()
![]()
![]() und
und ![]() ,
, ![]()
![]()
![]() .
.
Als trivialer Sonderfall ergibt sich, daß ![]() (also die Konklusion) immer
eine minimale Lösung des Rückschlußproblems ist, von der aber nur in
besonderen Fällen gebrauch gemacht werden sollte.
(also die Konklusion) immer
eine minimale Lösung des Rückschlußproblems ist, von der aber nur in
besonderen Fällen gebrauch gemacht werden sollte.
Der Vorteil der Minimalisierung der verborgenen Prämissen ist, daß nun auch im negativen Sinne entschieden werden kann, d.h., wenn man selbst diese minimalisierten verborgenen Prämissen nicht zugeben kann oder will, dann kann der Beweis nicht vervollständigt werden, dann war er nicht korrekt und muß überarbeitet oder aufgegeben werden.
Betrachtet man z.B. die Behauptung: Aus ,,Alle A sind B`` folgt ,,Alle C sind D``, so ist dieses ein unvollständiger Beweis. Eine mögliche Lösung für den Rückschluß auf verborgene Prämissen bei v. Freytag wäre ,,Alle C sind A`` und ,,Alle B sind D``, diese Lösung ist jedoch nicht minimal. Minimal wären jedoch ,,Alle C sind A oder D`` und ,,Alle B und C sind D``. Dieses nachzuweisen würde hier zu weit führen. Man sieht aber, daß diese Lösung schwächer ist als die v. Freytagsche.
Die Begriffslogik basiert auf den gleichen verbandstheoretischen Strukturen und Axiomen wie die Urteilslogik, jedoch ist sie allgemeiner, da ihr das zentrale Axiom der Urteilslogik fehlt, das Urteilsprinzip.
Die Begriffslogik ist ebenso wie die Urteilslogik schichtenartig aufgebaut. Auf der untersten Ebene sind die Grundobjekte Begriffe, die durch die Halbordnungsrelation des Art-Gattungs-Verhältnisses (der Identität) miteinander verbunden sind. Auf den darüberliegenden Ebenen sind die Objekte beliebige und beliebigstellige Relationen und Funktionen (unter anderen auch Urteile, obwohl sie nur als Begriffe behandelt werden, und demzufolge auch nicht im zweiwertigen Korsett der Urteilslogik stecken), die durch den Ableitungszusammenhang als Halbordnungsrelation miteinander verbunden sind.
Verallgemeinerte ,,und``- und ,,oder``-Operationen stehen in der Begriffslogik
(![]() und
und ![]() ) ebenso zur Verfügung, wie in der Prädikatenlogik der All-
und Existenzquantor. Variablen können beliebig indiziert werden, was der
) ebenso zur Verfügung, wie in der Prädikatenlogik der All-
und Existenzquantor. Variablen können beliebig indiziert werden, was der ![]() bzw.
bzw. ![]() , usw. Schreibweise der Prädikatenlogik entspricht.
, usw. Schreibweise der Prädikatenlogik entspricht.
Ausdruckstechnisch gesehen steht also inzwischen auch für die Begriffslogik das gesamte Operationsspektrum der Urteilslogik zur Verfügung. Der ,,mathematische`` Kalkülcharakter ist in keinster Weise mit dem Urteilsprinzip oder der Urteilslogik verbunden, die Begriffslogik kann genauso ,,genau`` sein, wie die Urteilslogik.
Der einzige Unterschied liegt in der schwächeren Axiomatik der Begriffslogik. Das ist aber kein Nachteil, im Gegenteil, oftmals ist die Urteilslogik zu stark, die begriffslogische Axiomatik würde zur Herleitung vieler Ergebnisse bereits ausreichen.
Methodisch gesehen sind allgemeinere (schwächere) Verfahren spezielleren Verfahren i.a. vorzuziehen, weil sie voraussetzungsärmer sind. Bei Bedarf ist es jederzeit möglich, den Kalkül zu verstärken. Vorschnelle Verstärkung birgt die Gefahr, geeignetere Darstellungsformen und feinere Ausdrucksformen von Beginn an auszuschließen.
Man könnte sich auch grundsätzlich in einem sehr allgemeinen Kalkül aufhalten, jedoch bestimmte Begriffe ,,höherer Schichten`` bzw. ,,Kategorien`` einführen, wie etwa ,,Begriff``, ,,Urteil``, ,,Individual-Begriff``, ,,Zweiwertig`` o.ä., so daß man bezüglich der Beweisbarkeit gewisser Formeln oder Regeln jeweils die entsprechenden ,,Kategorien`` angeben müßte, z.B.
Urteil(![]() ), Urteil(
), Urteil(![]() )
) ![]()
![]() oder
oder
Zweiwertig(![]() ), Zweiwertig(
), Zweiwertig(![]() ),
), ![]()
![]()
![]() etc.
etc.
Ebenso sollte man grundsätzlich zum Kalkülwechsel fähig sein. Semantische Netze, Venn-Diagramme, algebraische Kalküle, u.a. bieten in unterschiedlichen Situationen jeweils große Vorteile, aber auch Nachteile. Es ist also sinnvoll, sich jeweils den geeignetsten Kalkül für eine bestimmte Situation zu wählen. Einseitige Festlegungen auf einen bestimmten Kalkül bewirken eine Einengung, die den Blick auf bessere und einfachere Lösungen verstellen können.
Die Begriffslogik ist also keineswegs ,,unbrauchbar`` oder etwa ,,veraltet``, im Gegenteil, sie ist mindestens genauso modern und brauchbar wie die Urteilslogik. Beklagenswert ist allerdings das Informationsdefizit über die Möglichkeiten und Fähigkeiten der Begriffslogik.
Auch wenn Bruno Baron v. Freytag Löringhoff nun nicht mehr unter uns weilt, so werden sein Wirken in der Logik und seine Inspiration uns noch lange begleiten.
Aber nicht nur in der Logik, auch in anderen Gebieten wird man ihn nicht vergessen. Man denke hier nur an seine Arbeit im Rahmen des Schickardschen Nachlaßes, im besonderen an die Rekonstruktion der ersten Rechenmaschine von 1623.
Die Arbeit an der Begriffslogik wird weitergehen, denn auch wenn bereits ein erheblicher Teil der Grundlagenarbeit geleistet worden ist, so bleibt doch noch viel zu tun, z.B.:
Dennoch hat sich bereits jetzt eines recht deutlich ergeben: Die einseitige Bevorzugung der Urteilslogik in der heutigen Zeit ist lediglich eine historische Zufälligkeit, es hätte nicht so kommen müssen.
Andreas Otte, Oerlinghausen